אינוולוציה (מתמטיקה)

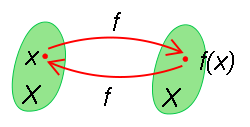
במתמטיקה, אינוולוציה היא פונקציה שהיא ההופכית של עצמה. כלומר, פונקציה חד-חד-ערכית בין שתי קבוצות $f:A\to B$, המקיימת את התכונה $f(f(x))=x$ לכל $x\in A$.

הפעלת אינוולוציה פעמיים מחזירה את האיבר המקורי

דוגמה יסודית לאינוולוציה היא הפעולה של לקיחת משלים של קבוצה, או הפעולה של שלילת פסוק לוגי. בתחומים מסוימים במתמטיקה יש לאינוולוציה משמעות מסוימת בהקשר בה היא מוגדרת. בתורת החבורות, למשל, כל איבר מסדר 2 הוא אינוולוציה (למעשה איבר $g\in G$ הוא אינוולוציה אם ורק אם ההומומורפיזם $x\mapsto gx$ הוא אינוולוציה כפונקציה).

תכונות

מן ההגדרה נובע שאינוולוציות הן תמיד פעולות אונאריות חד-חד-ערכיות. כלומר הן תמורות על תמונתן. תמורה היא אינוולוציה אם ורק אם בפירוק שלה למחזורים זרים מופיעים רק חילופים ונקודות שבת.

מספר האינוולוציות שמוגדרות על קבוצה סופית של n איברים נקרא מספר־טלפון ה-n-י. מספרים אלו מקיימים את נוסחת הנסיגה:

$a_{0}=a_{1}=1$

$a_{n}=a_{n-1}+(n-1)a_{n-2}$

הוכחה: נניח ללא הגבלת הכלליות שהקבוצה היא $\{1,\ldots ,n\}$. יש $a_{n-1}$ אינוולוציות שבהן n נקודת שבת (כל אינוולוציה כזו מתאימה לאינוולוציה אחת על $\{1,\ldots ,n-1\}$). יש $a_{n-2}$ אינוולוציות שבהן n עובר ל-$k\neq n$ (כל אינוולוציה כזו מתאימה לאינוולוציה אחת על $\{1,\ldots ,k-1,k+1,\ldots ,n-1\}$). יש $n-1$ ערכים אפשריים ל-$k\neq n$.

מספרי־הטלפון הראשונים הם: 1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496.

דוגמאות

• פונקציית הזהות היא אינוולוציה באופן טריוויאלי.
• הפונקציות הממשיות $-x$ ו-$x^{-1}$. אלו דוגמאות פרטיות לפעולת לקיחת הופכי בחבורה, שהיא תמיד אינוולוציה.
• באופן כללי פונקציה ממשית היא אינוולוציה אם ורק אם הגרף שלה סימטרי ביחס לישר y=x.
• פעולת ההצמדה של מספר מרוכב ופעולת השחלוף ופעולת הצמדה של מטריצה. אינוולוציות אלה הן במובן של תורת החוגים.
• מבין האיזומטריות של המישור האינוולוציות הן: פונקציית הזהות, כל שיקוף וכל סיבוב של 180 מעלות.
• פעולת השלילה בלוגיקה היא אינוולוציה. באופן דומה, כך גם פעולת המשלים בתורת הקבוצות. באופן כללי יותר, פעולת המשלים באלגברה בוליאנית היא אינוולוציה.
• הצפנה באמצעות מכונת אניגמה היא אינוולוציה – תהליך הפענוח של טקסט מתבצע על ידי הפעלה חוזרת של המכונה על הטקסט המוצפן.

קישורים חיצוניים

• אינוולוציה, באתר MathWorld (באנגלית)