בהסתברות ובסטטיסטיקה , התפלגות ריילי היא התפלגות רציפה, המתקבלת כאורך של וקטור דו-ממדי ששני רכיביו מתפלגים נורמלית , עם תוחלת אפס ואותה סטיית תקן . למשל, אם הסטיות של קליע מן המטרה מתפלגות נורמלית בציר X ובציר Y, ובלתי תלויות זו בזו, אז מרחק הקליע מן המטרה מתפלג לפי התפלגות ריילי.
התפלגות ריילי
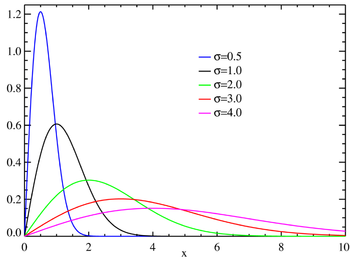
פונקציית צפיפות ההסתברות
פונקציית ההסתברות המצטברת
מאפיינים
פרמטרים
σ
{\displaystyle \ \sigma }
תומך
[
0
,
∞
)
{\displaystyle \ [0,\infty )}
פונקציית צפיפות הסתברות
x
σ
2
exp
(
−
x
2
2
σ
2
)
{\displaystyle \ {\frac {x}{\sigma ^{2}}}\exp(-{\frac {x^{2}}{2\sigma ^{2}}})}
פונקציית ההסתברות המצטברת
1
−
exp
(
−
x
2
2
σ
2
)
{\displaystyle \ 1-\exp(-{\frac {x^{2}}{2\sigma ^{2}}})}
תוחלת
π
2
⋅
σ
{\displaystyle {\sqrt {\frac {\pi }{2}}}\cdot \sigma }
סטיית תקן
4
−
π
2
σ
{\displaystyle \ {\sqrt {\frac {4-\pi }{2}}}\sigma }
חציון
σ
ln
(
4
)
{\displaystyle \sigma {\sqrt {\ln(4)}}\,}
ערך שכיח
σ
{\displaystyle \sigma \,}
שונות
4
−
π
2
σ
2
{\displaystyle {\frac {4-\pi }{2}}\sigma ^{2}}
אנטרופיה
1
+
ln
(
1
2
σ
3
)
+
γ
2
{\displaystyle 1+\ln \left({\frac {1}{{\sqrt {2}}\sigma ^{3}}}\right)+{\frac {\gamma }{2}}}
פונקציה יוצרת מומנטים
M
X
(
t
)
=
exp
(
μ
t
+
σ
2
t
2
2
)
{\displaystyle M_{X}(t)=\exp \left(\mu \,t+{\frac {\sigma ^{2}t^{2}}{2}}\right)}
צידוד
2
π
(
π
−
3
)
(
4
−
π
)
3
/
2
{\displaystyle {\frac {2{\sqrt {\pi }}(\pi -3)}{(4-\pi )^{3/2}}}}
גבנוניות
−
6
π
2
−
24
π
+
16
(
4
−
π
)
2
{\displaystyle -{\frac {6\pi ^{2}-24\pi +16}{(4-\pi )^{2}}}}
ההתפלגות תלויה בפרמטר
σ
{\displaystyle \ \sigma }
פונקציית הצפיפות היא
f
(
x
|
σ
)
=
x
exp
(
−
x
2
2
σ
2
)
σ
2
{\displaystyle f(x|\sigma )={\frac {x\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)}{\sigma ^{2}}}}
המומנטים נתונים על ידי
μ
k
=
σ
k
2
k
/
2
Γ
(
1
+
k
/
2
)
{\displaystyle \mu _{k}=\sigma ^{k}2^{k/2}\,\Gamma (1+k/2)\,}
כאשר
Γ
{\displaystyle \ \Gamma }
פונקציית גמא .
בפרט, מתקבלים:
התוחלת
σ
π
2
{\displaystyle \sigma {\sqrt {\frac {\pi }{2}}}}
השונות
4
−
π
2
σ
2
{\displaystyle {\frac {4-\pi }{2}}\sigma ^{2}}
הצידוד
2
π
(
π
−
3
)
(
4
−
π
)
3
/
2
{\displaystyle {\frac {2{\sqrt {\pi }}(\pi -3)}{(4-\pi )^{3/2}}}}
והגבנוניות
−
6
π
2
−
24
π
+
16
(
4
−
π
)
2
{\displaystyle -{\frac {6\pi ^{2}-24\pi +16}{(4-\pi )^{2}}}}
בהינתן מדגם בן N ערכים בלתי תלויים ושווי התפלגות מהתפלגות ריילי עם פרמטר
σ
{\displaystyle \sigma }
אומד הנראות המקסימלית של הפרמטר נתון על ידי הנוסחה
σ
^
=
1
2
N
∑
i
=
1
N
x
i
2
.
{\displaystyle {\hat {\sigma }}={\sqrt {{\frac {1}{2N}}\sum _{i=1}^{N}x_{i}^{2}}}.}
עריכה
בהינתן שיש בידינו משתנה מקרי u מהתפלגות אחידה רציפה סטנדרטית (בין 0 ל-1), אז למשתנה X המוגדר על ידי:
X
=
σ
−
2
ln
(
u
)
{\displaystyle X=\sigma {\sqrt {-2\ln(u)}}\,}
יש התפלגות ריילי עם פרמטר
σ
{\displaystyle \sigma }
דגימת ההעתקה ההופכית (ITS).
אם
X
,
Y
∼
N
(
0
,
σ
2
)
{\displaystyle \ X,Y\sim N(0,\sigma ^{2})}
R
=
X
2
+
Y
2
∼
R
a
y
l
e
i
g
h
(
σ
)
{\displaystyle \ R={\sqrt {X^{2}+Y^{2}}}\sim \mathrm {Rayleigh} (\sigma )}
סיגמא ).
אם
R
∼
R
a
y
l
e
i
g
h
(
1
)
{\displaystyle \ R\sim \mathrm {Rayleigh} (1)}
R
2
{\displaystyle \ R^{2}}
התפלגות כי בריבוע עם שתי דרגות חופש.
אם
X
{\displaystyle \ X}
התפלגות אקספוננציאלית ,
X
∼
E
x
p
o
n
e
n
t
i
a
l
(
x
|
λ
)
{\displaystyle \ X\sim \mathrm {Exponential} (x|\lambda )}
Y
=
2
X
σ
2
λ
∼
R
a
y
l
e
i
g
h
(
y
|
σ
)
{\displaystyle \ Y={\sqrt {2X\sigma ^{2}\lambda }}\sim \mathrm {Rayleigh} (y|\sigma )}
אם
R
∼
R
a
y
l
e
i
g
h
(
σ
)
{\displaystyle \ R\sim \mathrm {Rayleigh} (\sigma )}
∑
i
=
1
N
R
i
2
{\displaystyle \ \sum _{i=1}^{N}R_{i}^{2}}
התפלגות גמא עם הפרמטרים N ו-
2
σ
2
{\displaystyle 2\sigma ^{2}}
[
Y
=
∑
i
=
1
N
R
i
2
]
∼
Γ
(
N
,
2
σ
2
)
{\displaystyle \ [Y=\sum _{i=1}^{N}R_{i}^{2}]\sim \Gamma (N,2\sigma ^{2})}
התפלגות כי בריבוע , התפלגות רייס , התפלגות וייבול מהוות כולן הכללות של התפלגות ריילי.
התפלגות מקסוול-בולצמן היא התפלגות האורך של וקטור נורמלי תלת-ממדי, בדומה להתפלגות ריילי, המתאימה למקרה הדו-ממדי.
פונקציית הסיכון (Hazard function) של ההתפלגות ריילי היא ליניארית, וערכה הוא
h
(
x
)
=
x
σ
2
{\displaystyle h(x)={\frac {x}{\sigma ^{2}}}\!}
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 104 and 148, 1984
![{\displaystyle \ [Y=\sum _{i=1}^{N}R_{i}^{2}]\sim \Gamma (N,2\sigma ^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e56c371c187f3acf31e604548508b162e67ce1ea)
