משפט לז'נדר על משולשים כדוריים

בגאומטריה, משפט לז'נדר על משולשים כדוריים, שנקרא על שם אדריאן-מארי לז'נדר, מנוסח כדלהלן:

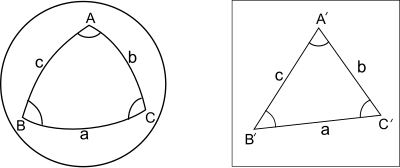
יהי ABC משולש כדורי על ספירת היחידה בעל צלעות קטנות a,b,c. יהי A'B'C' המשולש המישורי בעל אותן הצלעות. אז המשפט קובע שהזוויות של המשולש הכדורי עולות על הזוויות המתאימות של המשולש המישורי בזווית זהה בקירוב, ששווה לשליש ההפרש הזוויתי בין סכום הזוויות של המשולש הכדורי ל-π.

המשפט היה חשוב מאוד בפישוט החישובים הנומריים הסבוכים שנדרשו כדי לבצע סקרים גאודזיים מסורתיים (בעידן שלפני ה-GPS והמחשב) מבערך 1800 עד לאמצע המאה המאה ה-20.

לז'נדר לא היה הראשון לקבוע את המשפט, אולם היה הראשון לתת לו הוכחה, ב-1798.

משפט ז'יראר קובע שהסטייה הזוויתית של משולש כדורי, E, שווה לשטח שלו Δ, ולפיכך משפט לז'נדר ניתן לקביעה באופן הבא:

${\begin{aligned}A-A'\;\approx \;B-B'\;\approx \;C-C'\;\approx \;{\frac {1}{3}}E\;=\;{\frac {1}{3}}\Delta ,\qquad a,\;b,\;c\,\ll \,1.\end{aligned}}$

הסטייה הזוויתית, או השטח, של משולשים קטנים כאלה היא קטנה מאוד. לשם דוגמה נתייחס למשולש שווה-צלעות עם אורך צלע של 60km על פני ארץ כדורית בעלת רדיוס 6,371km; הצלע מתאימה למרווח זוויתי של 0.0094 = 60/6371, או בערך 10⁻² רדיאנים (זווית מרכזית של 0.57°). השטח של משולש כדורי כזה מקורב היטב עם זה של משולש מישורי עם אותן צלעות: ${\frac {1}{2}}a^{2}sin(\pi /3)=0.0000433$ רדיאנים.

כאשר אורכי הצלעות של המשולש עולים על 180km, הקשרים בין השטחים להבדלי הזוויות חייבים להיות מתוקנים על ידי איברים מסדר גבוה יותר:

${\begin{aligned}\Delta &=\Delta '\left(1+{\frac {a^{2}+b^{2}+c^{2}}{24}}\right),\\A&=A'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left(-2a^{2}+b^{2}+c^{2}\right),\\B&=B'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left({\quad a^{2}-2b^{2}+c^{2}}\right),\\C&=C'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left({\quad a^{2}+b^{2}-2c^{2}}\right).\end{aligned}}$

(כאשר Δ′ הוא שטח המשולש המישורי). תוצאה זאת הוכחה על ידי Buzengeiger ב-1818.

ניתן להכליל את המשפט לאליפסואיד כאשר a,b,c מחושבים על ידי חלוקת האורך האמיתי שלהן בשורש הריבועי של מכפלת רדיוסי העקמומיות הראשיים בנקודות מסוימות על הצלעות (במקום הרדיוס הכדורי). גאוס (1828, מאמרים 26-28) סיפק נוסחאות מדויקות במקרה זה. באותו חיבור, גאוס סיפק את ההכללה הבאה של משפט לז'נדר:

עבור משולש גיאודזי על משטח שרירותי מתקיים:

$A'=A-{\frac {1}{12}}(2\alpha +\beta +\gamma )\sigma$

$B'=B-{\frac {1}{12}}(\alpha +2\beta +\gamma )\sigma$

$C'=C-{\frac {1}{12}}(\alpha +\beta +2\gamma )\sigma$

כאשר $\alpha ,\beta ,\gamma$ הם הערכים של עקמומיות גאוס של המשטח בקודקודי המשולש A,B,C בהתאמה, ו- $\sigma$ הוא שטח המשולש.

ראו גם

• משפט ז'יראר