שילוש זווית

בגאומטריית המישור, בעיית שילוש הזווית (או טריסקציה של זווית) מבקשת לחלק זווית נתונה לשלושה חלקים שווים באמצעות סרגל ומחוגה. זוהי אחת מן הבעיות הגאומטריות של ימי קדם שלא נמצא לה פתרון במשך 2000 שנה. במאה ה-19 פותחה תורת גלואה שאפשרה להוכיח כי שילוש זווית אינו אפשרי באמצעות סרגל ומחוגה. למעשה, אפילו את הזווית של משולש שווה-צלעות לא ניתן לשלש בסרגל ומחוגה.

שילוש זווית באמצעות סרגל, מחוגה ו-neusis construction (כלי שבהינתן קטע, נקודה, ושני קווים, בונה נקודה על כל אחד מהקווים כך ששלוש הנקודות ― הנתונה ושתי החדשות ― נמצאות על ישר אחד, והמרחק בין שתי החדשות הוא כאורך הקטע הנתון).
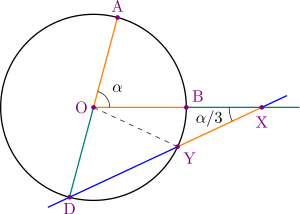
נתונה זווית (בכתום) שמרכזה O. בעזרת מחוגה, בונים מעגל (בשחור) שמרכזו O, וקרני הזווית חותכות אותו בנקודות A ו-B. בעזרת הסרגל (בירוק) ממשיכים את הקטע AO עד לחיתוך עם המעגל בנקודה D, ואת הקטע OB ממשיכים אל מחוץ למעגל. באמצעות neusis construction, מאתרים על המשך הישר OB ועל המעגל נקודות X,Y שנמצאות על ישר אחד עם הנקודה D, ושהמרחק ביניהן שווה לרדיוס המעגל (בכחול; הקטע שאורכו שווה לרדיוס המעגל מסומן בכתום. זו פעולה שלא ניתן לבצע בסרגל ומחוגה). הזווית BXY שווה לשליש הזווית AOB. הקטע המקווקו OY לא נדרש עבור הבנייה עצמה, אך בעזרתו ניתן להוכיח שהזווית שנבנתה היא אכן שליש של הזווית המקורית.

היתכנות שילוש הזווית

מאז תחילת המאה ה-19 ידוע שאי אפשר לשלש זווית בעזרת סרגל ומחוגה. קל לבנות זווית של $60^{\circ }$ כי זו הזווית הפנימית במשולש שווה-צלעות. כדי להוכיח שלא ניתן לשלש זווית בסרגל ומחוגה, מספיק להראות שלא ניתן לבנות זווית של $20^{\circ }$. נניח בשלילה שניתן לבנות זווית שכזו, אז ניתן לבנות קטע באורך $\cos(20^{\circ })$ בתור ניצב במשולש ישר-זווית עם זווית של $20^{\circ }$ ויתר באורך 1. מזהויות טריגונומטריות פשוטות נובע כי

$4\cos ^{3}(20^{\circ })-3\cos(20^{\circ })=\cos(60^{\circ })=0.5$

מכאן $\cos(20^{\circ })$ הוא שורש של הפולינום $8x^{3}-6x-1$. זהו פולינום אי פריק מעל השדה המספרים הרציונליים (כי בדיקה של כל המועמדים האפשריים תראה שאין לו שורש רציונלי). לכן $\cos(20^{\circ })$ הוא מספר אלגברי מדרגה 3, והשדה $\mathbb {Q} [\cos(20^{\circ })]$ הוא בעל ממד 3 מעל הרציונליים.

מספר מרוכב ניתן לבניה אם ורק אם הוא שייך לשדה בקצה שרשרת של הרחבות ריבועיות של הרציונליים (כי בניות בסרגל ומחוגה מתקבלות מחיתוכים בין ישרים ומעגלים שמניבים הרחבות ריבועיות). הממד של שדות כאלה הוא כמובן חזקת 2, אבל 3 אינו חזקה של 2, ומכאן שאי אפשר לבנות זווית של 20 מעלות.

שילוש זווית בכלים אחרים

עם זאת, אפשר לשלש זוויות אם נעזרים בכלים נוספים (מלבד סרגל ומחוגה):

• היפיאס (במאה החמישית לפני הספירה) הראה שבעזרת קוואדרטריקס ניתן לחלק זווית נתונה לשלושה חלקים, ולמעשה לכל מספר שלם של חלקים. (שמו של עקום זה בא לו מיכולתו לרבע את המעגל). שיטה זו ניתנת לתיאור נוסף: נניח ש- P נקודה על שפת מעגל ברדיוס R; המקום הגאומטרי של כל הנקודות המתקבלות מהמשכת הישר העובר ב-P דרך נקודה X על המעגל, למרחק של R, מאפשר לשלש כל זווית קטנה מ-135° אשר קודקודה הוא מרכז המעגל.
• ארכימדס הראה שאפשר, בעזרת סרגל, מחוגה ו-neusis construction (כלי שבהינתן קטע, נקודה, ושני קווים, בונה נקודה על כל אחד מהקווים כך ששלוש הנקודות ― הנתונה ושתי החדשות ― נמצאות על ישר אחד, והמרחק בין שתי החדשות הוא כאורך הקטע הנתון), לחלק זווית נתונה לשלושה חלקים. ראו איור משמאל.
• ניקומדס (במאה השנייה לפני הספירה) הראה שאפשר לשלש זווית אם נעזרים בקונכואידה.
• אטיין פסקל, אביו של בלז פסקל, הראה שאפשר לשלש את הזווית באמצעות קרדיואידה; שיטה זו דומה לשיטתו של ניקומדס.
• ניתן לשלש זווית על ידי קיפולי נייר

משפט מורלי

משפט מורלי: המשולש האדום הוא שווה-צלעות

משפט מורלי (שהתגלה על ידי פרנק מורלי (Frank Morley) ב-1904) קובע שאם משלשים את שלוש הזוויות של משולש, נקודות המפגש של הקרניים יוצרות משולש שווה-צלעות, כבאיור משמאל.

קישורים חיצוניים

מדיה וקבצים בנושא שילוש זווית בוויקישיתוף

• שילוש זווית, באתר MathWorld (באנגלית)