Theorema Elegantissimum
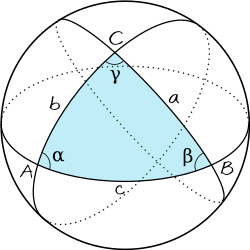
המשפט האלגנטי (בלטינית: Theorema Elegantissimum; תאורמה אלגנטִיסִימוּם) הוא משפט קלאסי בגאומטריה של משטחים, הנוגע לסכום הזוויות במשולש על פני משטח עקום. את המשפט, שהוא מקרה פרטי של משפט גאוס-בונה, הוכיח קרל פרידריך גאוס. המשפט קובע כי המגרעת הזוויתית של המשולש, כלומר ההפרש בין סכום זוויותיו ל-180 מעלות, שווה לאינטגרל על עקמומיות (עקמומיות גאוס) המשטח בתחום המשולש.

ניסוח מדויק עריכה
גאוס הוכיח שאם T הוא משולש גאודטי, אזי סכום זוויותיו הוא , כאשר הגודל הוא העקמומיות הכוללת (Total Curvature) של המשטח בתחום המשולש T. באופן כללי יותר, אם P הוא מצולע גאודטי בעל n צלעות, אזי סכום זוויותיו הוא .
מסקנות מן המשפט והכללות שלו עריכה
מסקנות:
- כמסקנה מן המשפט נובע שסכום הזוויות המרבי של משולש על פני כדור הוא 540 מעלות.
הכללות:
- משפט גאוס-בונה מכליל את המשפט למקרה שצלעותיו של המשולש אינן קווים גאודטיים של המשטח. משפט גאוס-בונה משלב בין רעיונות מגאומטריה דיפרנציאלית כמו עקמומיות גאוס ועקמומיות גאודטית לרעיונות מטופולוגיה כמו מאפיין אוילר לכדי קשר מתמטי עמוק ויוצא מן הכלל. משפט זה הוא הפרוטוטיפ של משפטי האינדקס שהתפתחו במאה ה-20.
משפט השטח של גאוס בגאומטריה היפרבולית עריכה
במקרה של גאומטריה היפרבולית עם עקמומיות גאוס שלילית קבועה (שניתן לתאר את התנהגותה על ידי אחד המודלים של המישור ההיפרבולי), גאוס נתן הוכחה גאומטרית סינתטית למשפט גאוס בונה במכתבו ליאנוש בולאי מ-1832, שעסק בגאומטריה לא-אוקלידית. במקרה זה משפט גאוס בונה קובע, בנוסף על כך שגם כאשר ההיקף של משולש שואף לאינסוף השטח שלו לעולם לא יכול לעלות על ערך מסוים (כלומר יש חסם עליון לשטח של משולש), שהגרעון הזוויתי פרופורציונלי במדויק לשטח. ההוכחה הסינתטית של גאוס לטענה זאת ראויה במיוחד לציון משום שהיא ניחנה באותה פשטות מושלמת שמאפיינת הוכחות לטענות כמו האי-רציונליות של שורש 2 או קיומם של אינסוף מספרים ראשוניים. במהותה ההוכחה מתבססת על הנחת ההומוגניות של המישור ההיפרבולי (עקמומיות אחידה או באופן שקול חסם עליון לשטח שאינו תלוי במיקום המשולש) ועל האקסיומה הבסיסית שמחליפה את אקסיומת המקבילים (שמאפיינת את הגאומטריה ההיפרבולית). הטיעון שלו מורכב מ-7 חלקים (המחשות גאומטריות לטיעון מופיעות במאמר שהובא ברשימת המקורות):
1. שלושה ישרים, מקבילים בזוגות בכיוונים מנוגדים, יוצרים משולש אסימפטוטי T (שכל זוויותיו אפס).
2. ל-T יש שטח סופי, שנסמנו t (שאם לא כן הגאומטריה היא אוקלידית).
3. ישר de ושתי קרניים מקבילות לו היוצאות מנקודה חיצונית a יוצרות משולש ששתיים מזוויותיו אפס, אשר השטח שלו הוא פונקציה של הזווית החיצונית למשולש בקודקוד a (בלבד!), אשר עולה מ- ל- .
4. התייחסות למשולש אסימפטוטי, תוך הצבת הקודקוד a על אחת מצלעות המשולש האסימפטוטי, מאפשרת לייצר שני משולשים מהסוג שהוגדר בסעיף 3 (אשר שתיים מזוויותיהם אפס). סכום השטחים של שני המשולשים הללו שווה לזה של המשולש האסימפטוטי (שסימנו אותו t), לכן: .
5. הצבת הנקודה a בתוך המשולש (לא על צלעותיו) מאפשרת, בדומה לסעיף 4, לייצר שלושה משולשים ששתיים מזוויותיהם אפס (באמצעות העברת מקבילים מנקודה זו לכל אחת מצלעות המשולש), ולכן מתקיים: . סעיף זה למעשה עושה שימוש מהותי באקסיומה הבסיסית שמאפיינת את הגאומטריה ההיפרבולית: דרך כל נקודה מחוץ לישר נתון ניתן להעביר לפחות שני ישרים מקבילים לו.
6. מכיוון ש-: , אז מתקיים ש-: , וערכו של קבוע זה הוא .
7. ניתן לפרק את המשולש האסימפטוטי T למשולש סופי ABC בעל שטח שנסמנו Z ושלושה משולשים ששתיים מזוויותיהם אפס. הזוויות החיצוניות לשלושת המשולשים הללו הם הזוויות הפנימיות של המשולש הסופי (המשולש הרביעי) A,B,C, לכן אם נסמן את שטחיהם באותיות , אז מתקיים:
ומכאן נקבל:
ובכך תמה ההוכחה.
מקורות עריכה
- Dictionary of Analysis, Calculus and Differential Equations, Douglas N. Clark.
- [1](הקישור אינו פעיל) ,Gauss as a geometer
H.S.M.Coxeter