הנפה של ארטוסתנס

בתורת המספרים, הנָפָה של אֵרָטוֹסְתֶנֶס הוא אלגוריתם פשוט ויעיל למציאת כל המספרים הראשוניים עד למספר שלם מסוים. המצאת הנפה מיוחסת למתמטיקאי היווני ארטוסתנס.

מציאת כל המספרים הראשוניים בין 2 ל-120 באמצעות הנפה של ארטוסתנס, כשהסימון מתחיל ממספר בריבוע.

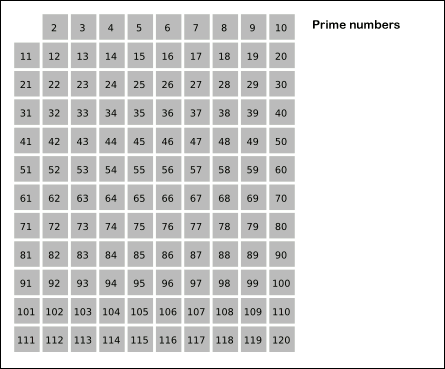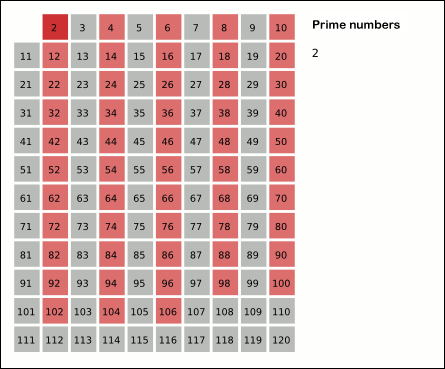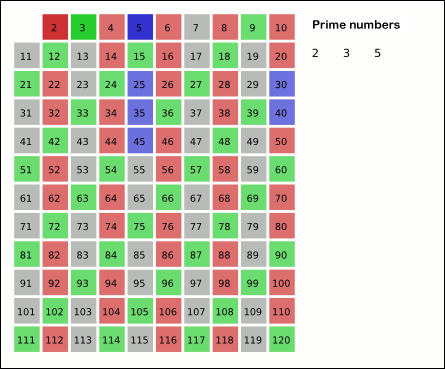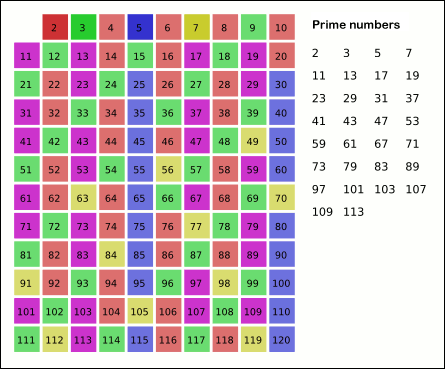
מתחילים עם רשימת כל המספרים השלמים מ-2 ועד המספר הנבחר n. בכל שלב, מכריזים על המספר הקטן ביותר הלא מסומן ברשימה שעוד לא טופל כעל מספר ראשוני, ומסמנים בתוך הרשימה את כל הכפולות שלו (שהם יהיו מספרים פריקים). ממשיכים לבצע שלב אחרי שלב, כל עוד זה אפשרי.

בסופו של התהליך, כל המספרים ברשימה שלא סומנו הרי הם כל המספרים הראשוניים מ-2 עד n.

את הכפולות מוצאים על ידי ספירה מהמספר כלפי מעלה בצעדים של אותו מספר. למשל, עבור 3: 6, 9, 12, 15, ... . יהיו גם מספרים שיסומנו יותר מפעם אחת, למשל 15 = 3 * 5 = 5 * 3. לכן את הספירה ניתן להתחיל מהמספר בריבוע (למשל 9 עבור 3, מכיוון ש 6 כבר יהיה מחוק בספירה מ 2). כמו כן ניתן לעבוד עם המספרים האי־זוגיים בלבד ולספור בצעדים כפולים, למשל עבור 5: 25, 35, 45, 55, ... .

את המספר 1 אין כוללים ברשימה, משום שהוא לא נחשב לראשוני. ראו מספר ראשוני להסבר בעניין זה.

דוגמה

להלן פעולות האלגוריתם עבור המספרים מ-2 עד 20.

• רושמים את המספרים מ-2 ואילך, עד לגבול שקבענו מראש:

   2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 

• 2 הוא המספר הראשוני הראשון. סופרים מ-4 בצעדים של 2 ומסמנים את המספרים האלה:

   2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 
       ^   ^   ^   ^     ^     ^     ^     ^     ^

• המספר הבלתי מסומן הראשון מעל 2 ברשימה הוא 3, המספר הראשוני הבא. סופרים מ-9 בצעדים של 3 ומסמנים:

   2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 
       -   -   - ^ -     -^    -  ^  -     -^    -

• המספר הבלתי מסומן הראשון מעל 3 ברשימה הוא 5. הספירה אמורה להתחיל מ-25 אך מספר זה גדול מ-20. לכן אנו מסיימים. המספרים הבלתי מסומנים ברשימה כעת הם הם כל המספרים הראשוניים מ-2 עד 20:

   2 3   5   7        11    13          17    19

הסימנים שסימנו במהלך הפעולה מהווים את החורים בנפה שדרכם עוברים המספרים הפריקים כך שבסוף נשארים בה רק המספרים הראשוניים.

פסאודו קוד של נפת ארטוסתנס

algorithm Sieve of Eratosthenes is
    input: an integer n > 1.
    output: all prime numbers from 2 through n.

    let A be an array of Boolean values,
      indexed by integers 2 to n,
      initially all set to true.
    
    for i = 2, 3, 4, 5, ..., not exceeding √n do
      if A[i] is true
        for j = i², i² + i, i² + 2i, i² + 3i, ..., not exceeding n do
          assign A[j] := false

    return all i such that A[i] is true.

או בצורה סימבולית,

 primes = [2,3..] \ [ p²,p²+p,... for p in primes ]

קוד לנפת ארטוסתנס בשפת פייתון

import math

def all_primes(n):
    lst = [True] * (n - 2)
    for i in range(2, int(math.sqrt(n) + 1)):
        if lst[i - 2]:
            for j in range(i ** 2, n, i):
                lst[j - 2] = False
    return [m + 2 for m in range(len(lst)) if lst[m]]

ראו גם

• הנפה של אטקין

קישורים חיצוניים

מדיה וקבצים בנושא הנפה של ארטוסתנס בוויקישיתוף

• הורדת יישום הפועל לפי שיטת הנפה של ארטוסתנס. (12KB, דורש Microsoft .NET framework, גרסה 4.0 לפחות)
• ארי שביב, הנפה של ארטוסתנס, באתר מכון דוידסון, אוקטובר 2014(הקישור אינו פעיל, 06/10/2023)
• הנפה של ארטוסתנס, באתר MathWorld (באנגלית)
• הנפה של ארטוסתנס, באתר אנציקלופדיה בריטניקה (באנגלית)