Spline

במתמטיקה, Spline (פוּנְקְצִיַּת-אִפּוּץ) הוא פונקציה המוגדרת על תמך סופי על ידי קבוצה של פונקציות בסיס פולינומיות רציפות למקוטעין. פונקציות הבסיס נבחרות כך שהן חלקות בכל מקום פרט למספר סופי של נקודות החיבור בין מקטעי הפולינומים. נקודות החיבור מכונות קשרים (באנגלית knots).. פולינומים אלו נבחרים כך שבנקודת הקשר ערכיהם וערכי נגזרותיהם עד סדר הפולינום שוות מצידיו של הקשר. פונקציות spline מאופיינות בצורה חד ערכית על ידי דרגתן ווקטור הקשרים שלהן.

Spline ריבועי מורכב משישה מקטעי פולינום. בין הנקודה 0 לנקודה 1 קו ישר. בין נקודה 1 לנקודה 2 פרבולה עם נגזרת שנייה = 4. בין נקודה 2 לנקודה 3 פרבולה עם נגזרת שנייה = -2. בין נקודה 3 לנקודה 4 קו ישר. בין נקודה 4 לנקודה 5 פרבולה עם נגזרת שנייה = 6. בין נקודה 5 לקודה 6 קו ישר.

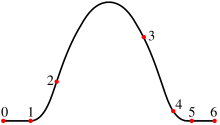
לפונקציות spline שימושים רבים, לדוגמה, בחישוב קרובים לפונקציות על ידי אינטרפולציה, אינטרפולציית spline מועדפת לעיתים קרובות על אינטרפולציה פולינומית מפני שהיא מניבה תוצאות דומות ובו בעת נמנעת מבעיית חוסר היציבות הנובעת מתופעת רונגה המתרחשת בעת שימוש בפולינומים מסדר גבוה.

בנוסף לשימוש הישיר בפונקציות ספליין לקרובים, שימוש נפוץ בהם הוא כפונקציות בסיס לתיאור עקומים פרמטריים הידועים גם בשם B-spline. לדוגמה, בגרפיקה ממוחשבת, עקומות b-spline פופולריות עקב פשטות בנייתן, קלות השימוש בהן ודיוקן. בנוסף, היכולת של עקומות b-spline לשערך צורות מורכבות ועיצוב עקומות אינטראקטיבי הופך אותן לנפוצות בישומי עיצוב גרפי. בישומים מעשיים מקובל להשתמש בספליינים מסדר שני ושלישי ( Quadratic and cubic splines), כלומר, מסדר 3,2.

אטימולוגיה

מקור השם: רצועת המתכת המשמשת מעצבים - "Flat Spline"

המונח Spline אומץ על שם רצועה גמישה של מתכת המשמשת בדרך כלל מעצבים לסייע בציור עקומה מעוגלת. סרגלים מעוקמים כאלה שימשו בעבר בתכן של גופים בעלי צורות גאומטריות חלקות, למשל, קוער של ספינות. בעידן המודרני מקובל לראות במאמר מ 1946 של Schoenberg את הניסוח המתמטי הראשון.

$S(t)={\begin{cases}{\frac {1}{4}}(t+2)^{3}&-2\leq {t}\leq -1\\{\frac {1}{4}}\left(3|t|^{3}-6t^{2}+4\right)&-1\leq {t}\leq 1\\{\frac {1}{4}}(2-t)^{3}&1\leq {t}\leq 2\end{cases}}$

הגדרה

spline היא פונקציה פולינומית ממשית חלקה למקוטעין

$S\colon [a,b]\to \mathbb {R}$

תחום סגור $[a,b]$ המורכב מ-$k$ מקטעים $[t_{i-1},t_{i}]$ כאשר $a=t_{0}<t_{1}<\dotsb <t_{k-1}<t_{k}=b$.

ההגבלה של $S$ במקטע $i$ הוא פולינום

$P_{i}\colon [t_{i-1},t_{i}]\to \mathbb {R}$,

כך ש:

$S(t)={\begin{cases}P_{1}(t){\mbox{, }}t_{0}\leq t<t_{1}\\P_{2}(t){\mbox{, }}t_{1}\leq t<t_{2}\\\vdots \\P_{n}(t){\mbox{, }}t_{n-1}\leq t<t_{n}\\\end{cases}}$

הסדר הגבוה ביותר של פולינומים $P_{i}(t)$ נקרא סדר ה spline - $S$. כאמור, spline אחיד (uniform) אם כל תת-המקטעים באותו אורך במרחב הפרמטרי ולא אחידה אחרת.

הרעיון הוא לבחור פולינומים באופן המבטיח חלקות מספקת ל $S$. באופן ספציפי, spline מסדר $n$,‏ $S$ נדרש להיות רציף וגזיר $n-1$ פעמים בנקודות הפנימיות $t_{i}$: ל $i=1,\dotsc ,k-1$ ו $j=0,\dotsc ,n-1$

$P_{i}^{(j)}(t_{i})=P_{i+1}^{(j)}(t_{i})$.

דוגמאות

דוגמה פשוטה של spline ריבועי (מסדר 2)

$S(t)={\begin{cases}(t+1)^{2}-1&-2\leq t<0\\1-(t-1)^{2}&0\leq t\leq 2\end{cases}}$

אשר בה $S'(0)=2$.

דוגמה פשוטה של cubic spline היא

$S(t)=\left|t\right|^{3}$

או

$S(t)={\begin{cases}t^{3}&t\geq 0\\-t^{3}&t<0\end{cases}}$

ו

$S'(0)=\ 0$

$S''(0)=\ 0$

דוגמה של שימוש ב cubic spline כדי ליצור עקומת פעמון של פולינומי הפצה של ארווין-הול:

B-splines

B-splineמישורי

ביישומים בהם פונקציית ספליין אחת אינה שימושית ניתן להשתמש בסכום ממושקל (weighted-sum) של פונקציות בסיס על מנת לתאר עקומים מורכבים. ברישום מקובל $C(t)=\sum _{i}P_{i}\cdot B_{i}^{d}(t)$ כאשר $C(t)$ פרמטרי ב $t$, $d$ דרגת הספליין ונקודות הבקרה $P_{i}\in R^{n}$ מגדירות את הטווח של העקום, לשם פשטות השמטנו את וקטור הקשרים הדרוש להגדרה מלאה של פונקציות הבסיס. לדוגמה, עבור עקום מישורי, נקודות הבסיס שוכנות במישור ו$n=2$.

תכונות B-Spline

1. חלוקת היחידה - partition of unity - עבור וקטור קשרים ${\cal {{t}=\{t_{i}\}_{i=0}^{N}:{\cal {{t}\in [t_{k-1},t_{N-k+1}]}}}}$, $\sum _{i=0}^{N-k}B_{i,k}(t)=1,\forall {k}>0$. אינטואיטיבית, בדומה לפונקציות בזייה(bezier), סכום כל פונקציות הבסיס לכל נקודה בה הפונקציות מוגדרות יהיה 1.
2. הכלה בקמור - convex hull property - העקום מול בקמור של נקודות הבקרה.
3. הפחתת שינויים - Variation diminishing, בדומה לעקומי בזייה גם בעקומי b-spline, אם נחתוך את העקום המוגדר ביחס לאוסף נקודות הבקרה ווקטור הקשרים מספר החיתוכים של הקו הישר יהיה שווה או קטן ממספר החיתוכים של הקו עם הפוליגון הנוצר מחיבור נקודות הבקרה בקוים ישרים.
4. תמך סופי - local support - שינוי במיקום של נקודת בקרה ישנה קטע סופי בעקום.

קישורים חיצוניים

מדיה וקבצים בנושא Spline בוויקישיתוף

• תורת ספליין, דף שער בספרייה הלאומית
• Spline, באתר MathWorld (באנגלית)