חוק גאוס
|
עיינו גם בפורטל פורטל הפיזיקה מהווה שער לחובבי הפיזיקה ולמתעניינים בתחום. בין היתר, בפורטל תוכלו למצוא מידע על פיזיקאים חשובים, על ענפי הפיזיקה ועל תאוריות פיזיקליות. |
חוק גאוס הוא חוק יסודי באלקטרוסטטיקה, המבטא את הקשר בין שדות חשמליים והתפלגות מטענים חשמליים. החוק מוכל במשוואות מקסוול, המהוות את התשתית לתורת החשמל והמגנטיות הקלאסית. חוק גאוס קובע כי סך השטף החשמלי דרך מעטפת סגורה נמצא ביחס ישר למטען החשמלי הכלוא בתוך המעטפת.

החוק נוסח לראשונה[1] על ידי ז'וזף לואי לגראנז' בשנת 1773[2], ובעקבותיו נוסח על ידי קרל פרידריך גאוס בשנת 1813[3]. אצל שניהם היה זה בהקשר לעבודתם על כוחות משיכה בין אליפסואידים. החוק נגזר מחוק קולון, חוק ניסיוני המתאר את המשיכה בין מטענים חשמליים נקודתיים. ניסוחו המתמטי של החוק מופיע בשתי צורות – בצורה דיפרנציאלית ובצורה אינטגרלית. שתי הצורות מקושרות על ידי משפט גאוס (משפט הדיברגנץ), משפט מתמטי מתחום האנליזה הווקטורית. כמו כן, לחוק גאוס ישנן מקבילות בחוקי פיזיקה של כוחות השונים מהכוח החשמלי, זאת מכיוון שמבחינה מתמטית ניתן לנסח חוק המקביל לחוק גאוס לכל כוח ריבועי הפוך, כגון כוח הכבידה.
מבוא אינטואיטיבי עריכה
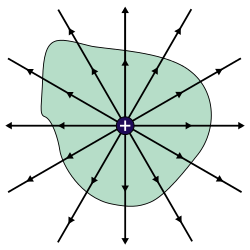
שטף הוא רעיון מתמטי תאורטי המגדיר באופן כמותי תכונה חדשה לגורם בעל כיוון העובר דרך משטח. דוגמאות לגורם כזה הן מהירות מים, קרינה היוצאת ממנורה או חום המתפשט מתגובה כימית. מתמטית, השטף הוא מכפלה סקלרית בין גודל הווקטור המייצג את הגורם, לבין וקטור המייצג משטח בו הגורם פוגע. לשטף משמעויות פיזיקליות שונות בהתאם לגורם עליו הוא מוגדר. לדוגמה, עבור זרם מים, השטף מייצג את כמות המים העוברת דרך משטח כלשהו ליחידת זמן. בחוק גאוס, השטף מתייחס להיטל של וקטור השדה החשמלי הפועל על משטח מסוים, על הווקטור המייצג את המשטח (הווקטורים מוכפלים סקלרית אחד בשני).
גודלו של השטף על מעטפת סגורה, כאשר מקור השטף חיצוני למעטפת, הוא אפס. אינטואיטיבית, ניתן לדמיין את השטף כקצב הזרימה של מים העוברים דרך מסגרת (שלד) של תיבה. אם מגדירים את כמות המים שיוצאים מתוך המסגרת כשלילית, ואת כמות המים הנכנסים למסגרת כחיובית, ונתון כי ספיקת המים אחידה, אז כמות המים שתעבור דרך המסגרת ביחידת זמן תהיה שווה לכמות המים שתספיק לצאת מהמסגרת. לכן השטף הכולל בתיבה, כאשר הזרימה חיצונית לה, הוא אפס. תכונה זו אינה תלויה בגודל התיבה, צורתה או עיוותה של המסגרת במרחב וכדומה. כמות המים הנכנסים והיוצאים לא תשווה לאפס רק כאשר זרם המים מתחיל בתוך התיבה, או ששואבים מים מהתיבה בקצב שונה מקצב זרימת המים.
חוק גאוס קובע כי השטף של שדה חשמלי העובר דרך מעטפת סגורה, הוא פרופורציוני למטען בתוך המעטפת. על כן, שימוש במושג השטף יכול לעזור בחישוב השדה החשמלי בקלות יחסית, במיוחד כאשר הבעיה כוללת צורות סימטריות שיוצרות את השדה החשמלי.
פיתוח מתמטי עריכה
חוק גאוס פותח מתוך חוק קולון, חוק ניסיוני המנסח את גודל הכוח החשמלי הפועל בין מטענים בודדים.
חוק גאוס הוא למעשה הכללה של חוק קולון למספר רב של חלקיקים הנמצאים בתוך מעטפת סגורה. בתכלית, הרעיון הוא להעביר את חוק קולון לצורה של סכימה (אינטגרציה), מה שמאפשר לחשב כוח או שטף באזורים או שטחים (הנמצאים בתוך המעטפת) אשר מכילים מטענים בודדים רבים, שכן לא ניתן לחשב את סך הכוחות בין כל חלקיק וחלקיק בעזרת חוק קולון עבור מטענים רבים.
הגדרת השטף והשטף החשמלי עריכה
השטף (Flux) על משטח הוא תכונה של כל שדה וקטורי, אשר מספק מידה לעוצמת השדה החודר משטח הנמצא בשדה. מבחינה פורמלית, השטף מוגדר כמכפלה סקלרית בין השדה הווקטורי (שמייצג את הגורם שעובר דרך המשטח) לבין וקטור השטח עצמו. וקטור השטח הוא וקטור הניצב למשטח וגודלו הוא כגודל המשטח.
הגדרת השטף: .
בחישובים הנעזרים בחוק גאוס משתמשים במושג היסוד משטח גאוסי. משטח גאוסי הוא מעטפת סגורה במרחב. כלומר, אי אפשר להיכנס לתוכה בלי לחדור אותה. על מנת לשמור על פורמליזם, הוגדר השטף הנכנס למשטח גאוסי כשטף חיובי, והשטף היוצא ממנו הוגדר כשלילי. כתוצאה מכך מתחייב כי כיוון וקטור המשטח פונה החוצה מן המשטח הגאוסי. תכונה של משטח גאוסי היא שכאשר מקור המשרֶה שדה וקטורי כלשהו אינו נמצא בתוך המשטח הגאוסי, השטף הכולל העובר בתוך המשטח הגאוסי יהיה אפס. זאת מכיוון שכל קו מן השדה הווקטורי – השדה החשמלי במקרה זה – שנכנס למשטח, גם יוצא ממנו. לכן התרומה הכוללת לשטף היא אפס, אחרת היו קווי שדה שנקטעים בתוך המשטח, מה שסותר את תכונת רציפות השדה.
חישוב השטף החשמלי הפועל על משטח גאוסי עריכה
כיוון שכיוונו של ווקטור המשטח משתנה כתלות במיקום על המשטח הגאוסי, לא ניתן להתייחס למשטח כולו כאל יחידה אחת. כמו כן גם וקטור הכוח יכול להשתנות כתלות במיקום. על כן, כדי לחשב את השטף נחלק את המשטח לפיסות קטנות כרצוננו עד אשר כיפופו יהיה ניתן להזנחה, והשינוי בשדה הווקטורי עליו יהיה זניח גם הוא. לבסוף, נסכום את המכפלות הסקלריות בין כל פיסה אינפיניטסימלית לבין השדה. כאשר גודל חתיכות המשטח שואף לאפס, הסכום הופך לאינטגרל משטחי כדלהלן:
חישוב שטף לפי הגדרה דרך מעטפת המקיפה מטען עריכה
באמצעות חוק קולון ניתן לחשב את השטף החשמלי סביב מעטפת כדורית היפותטית העוטפת מטען. עבור כל נקודה במרחק שווה מן המטען החשמלי, השדה החשמלי הוא באותו גודל קבוע וכיוונו רדיאלי, כלפי חוץ, ולכן הזווית בינו לבין וקטור המשטח היא אפס. מכאן: .
סכום כל חלקיקי השטח הוא שטח כלל המעטפת בגודל R ששטחה .
מכאן: . זהו גודל קבוע אשר תכונה מהותית בו היא שהוא לא תלוי כלל בגודל המעטפת.
גזירת החוק עריכה
הודות לתכונה שהוכחה לעיל ניתן לומר שללא תלות בגודל המעטפת כאשר מדובר במשטח גאוסי השטף של מטען בודד דרכו הוא פרופורציוני למטען שבתוכו. משימוש בעקרון הסופרפוזיציה של הכוח החשמלי ניתן להפריד כל סט של מטענים למטענים בדידים ולהכיל עליהם את המשפט הנ"ל. מכאן שהשטף הכולל יהיה סכום השדות הפועלים על אותם פיסות המשטח. לכן ניתן לומר כי השטף הכולל הוא סכום כלל השטפים החלקיים, ואם כל שטף חלקי פרופרציוני למטען המשרה אותו משמע שהשטף הכולל פרופרציוני גם הוא למטענים המשרים אותו, וזהו החוק של גאוס לשטף חשמלי. כאשר בניסוח המקובל נעשה שימוש במקדם דיאלקטריות הריק תוך המרת הקבועים שהוצגו לעיל כך:
חוק גאוס בניסוח אינטגרלי עריכה
הניסוח המתמטי של החוק בצורתו האינטגרלית הוא:
כאשר הוא השטף החשמלי, הוא השדה החשמלי, הוא אלמנט שטח אינפיניטסימלי על המשטח הסגור , אשר כיוונו מוגדר כניצב למשטח, כלפי חוץ, הוא המטען הכלוא בתוך המשטח, הוא צפיפות המטען החשמלי בנקודה , הוא קבוע דיאלקטריות הריק ו־ הוא אינטגרל על המשטח הגאוסי התוחם את נפח .
יש לשים לב כי הווקטור מאונך למעטפת, והשדה החשמלי מוכפל סקלרית בווקטור זה; ככל שקווי השדה מאונכים יותר למעטפת, כך השטף החשמלי גדול יותר.
חוק גאוס בניסוח דיפרנציאלי עריכה
ניסוחו של חוק גאוס בריק בצורתו הדיפרנציאלית הוא:
כאשר הוא אופרטור הדיברגנץ ו- היא צפיפות מטען נפחית. החוק מקשר בין דיברגנץ השדה החשמלי בנקודה במרחב לבין צפיפות המטען באותה הנקודה. בחומר, מקדם הדיאלקטריות שונה מ- (המקדם הדיאלקטרי של הריק).
שקילות הניסוחים עריכה
ניתן להוכיח באמצעות משפט גאוס (משפט הדיברגנץ) ששני הניסוחים – האינטגרלי והדיפרנציאלי – שקולים מתמטית:
הניסוח האינטגרלי של חוק גאוס:
עבור כל משטח גאוסי הכולא בתוכו מטען Q.
לפי משפט גאוס, משוואה זו שקולה לזו:
עבור כל נפח V המכיל מטען Q.
המטען בתוך הנפח שווה לצפיפות המטען הנפחית של הנפח כפול הנפח:
כדי שמשוואה זו תהיה נכונה תמיד עבור כל נפח V כלשהו, האינטגרנדים בשני אגפי המשוואה צריכים להיות שווים. ולפיכך, משוואה זו שווה ערך לזו:
מ.ש.ל.
חוק גאוס למגנטיות עריכה
- ערך מורחב – חוק גאוס למגנטיות
בנוסף לחוק גאוס עבור השדה החשמלי, קיים גם חוק גאוס עבור השדה המגנטי. בניסוח האינטגרלי החוק נכתב כך: .
פירוש נוסחה זו הוא כי סך השטף המגנטי דרך כל מעטפת סגורה שווה ל-0. גם כאן ניתן להשתמש במשפט גאוס על מנת לעבור לצורה הדיפרנציאלית של החוק: .
המשמעות של חוק זה היא שאין לשדה המגנטי מקורות. כלומר, קווי השדה אינם יוצאים או נכנסים לנקודה כלשהי במרחב, אלא יוצרים לולאות סגורות. תכונה זאת קשורה לכך שלפי כל התצפיות שנעשו עד כה, לא קיימים בטבע מונופולים מגנטיים – לצד כל קוטב מגנטי צפוני קיים קוטב דרומי (ולהפך), והם אינם ניתנים להפרדה.
שני החוקים מהווים חלק ממשוואות מקסוול.
קישורים חיצוניים עריכה
הערות שוליים עריכה
- ^ Duhem, Pierre. Leçons sur l'électricité et le magnétisme (in French). vol. 1, ch. 4, p. 22–23. shows that Lagrange has priority over Gauss. Others after Gauss discovered "Gauss' Law", too.
- ^ Lagrange, Joseph-Louis (1773). "Sur l'attraction des sphéroïdes elliptiques". Mémoires de l'Académie de Berlin (in French): 125.
- ^ Gauss, Carl Friedrich. Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata (in Latin). (Gauss, Werke, vol. V, p. 1). Gauss mentions Newton's Principia proposition XCI regarding finding the force exerted by a sphere on a point anywhere along an axis passing through the sphere.