ניווט יחסי
| יש להשלים ערך זה: בערך זה חסר תוכן מהותי. ייתכן שתמצאו פירוט בדף השיחה. | |
| יש לערוך ערך זה. הסיבה היא: ויקיזציה. | |
ניווט יחסי (באנגלית: PN - Proportional Navigation) הוא חוק הנחיה שנעשה בו שימוש בטילים (לרוב בטיל נגד מטוסים או נגד טילים).
חוק ההנחיה מתבסס על העובדה ששני אלמנטים נמצאים במסלול התנגשות אם קו הראייה (LOS - Line-of-Sight) הישיר שלהם לא משנה כיוון. שיטת הניווט היחסי קובעת שוקטור המהירות של הטיל צריך להסתובב בקצב פרופורציונלי לקצב הרוטציה של קו הראייה, ובאותו כיוון. בניסוח מתמטי, משמעות הדבר היא:
כאשר היא התאוצה האנכית לוקטור מהירות הטיל הרגעי, N הוא קבוע פרופורציונליות חסר ממדים שנקרא קבוע הניווט ונע בדרך כלל בין 3 ל-5, הוא קצב הסיבוב של קו הראייה, ו-V היא מהירות הסגירה. משמעות השם "ניווט יחסי" היא שהניווט יחסי במובן שהוא פרופורציונלי לשינוי באוריינטציה היחסית (כלומר זווית קו הראייה) של הטיל והמטרה במרחב. במילים פשוטות, חוק הניווט היחסי קובע כי על העצם המנווט לנווט בהתאם לשינוי במיקום הנצפה (במובן של מיקום זוויתי - מיקום על פני הספירה השמיימית), ולא בהתאם למיקום האקטואלי של המטרה באותו רגע. ההיגיון העומד מאחורי החוק הוא שהעצם המנווט צריך לנווט (לפנות) בשיעור פרופורציונלי לסיבוב קו הראייה כי ככל שסיבוב קו הראייה מהיר יותר הדבר מעיד על כך שהעצם המנווט צריך "לסגור" פער גדול יותר מבחינת רכיב המהירות הניצב לקו הראייה על מנת להיות בנתיב התנגשות עם המטרה. השינוי בין גישה זו להנחית טילים לעומת ההנחיה הקלאסית (קרי הנחית מרדף) היווה את המהפך שעמד מאחורי ההצלחה של הטילים המונחים הראשונים (היסטורית אלגוריתם הנחיה חדשני זה יושם לראשונה בטיל ה-AIM 9 Sidewinder).
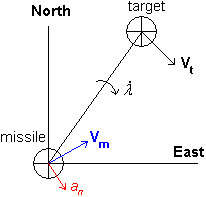
לדוגמה, אם קו הראייה מסתובב קלות מצפון למזרח, הטיל צריך לפנות ימינה בפקטור מסוים מהר יותר מקצב הסיבוב של קו הראייה. פקטור זה נקרא קבוע הניווט.
לניווט יחסי, על אף פשטותו היחסית, מספר מאפיינים משותפים עם חוקי הנחיה אופטימלית; אחד מהם הוא שחוק הנחיה זה משיג מרחק החטאה אפסי במאמץ בקרה מינימלי (במקרה של מטרה לא מתמרנת). מאז הצגת החוק בערך בשנות ה-40 ויישומו בפיתוח הדגמים המוצלחים הראשונים של הטילים המונחים, מחקרים רבים נערכו על המאפיינים של חוק הנחיה זה מהיבטים רבים: מבחינת הקינמטיקה (התאוצות הנדרשות) של המסלולים המתקבלים, מבחינת הבקרה, ועוד. הספרות הענפה התומכת בחוק הנחיה זה היא הבסיס לתפוצתו הרחבה בעולם, ולהיותו אחד משיטות ההנחיה היעילות והנפוצות ביותר.
היסטוריה
עריכהנטען ששיטת הניווט היחסי הייתה ידועה למדענים גרמנים בפנמינדה (Peenemunde) ושהם פיתחו את המשוואות הבסיסיות והעקרונות של ניווט יחסי עם סיום מלחמת העולם השנייה. אף על פי כן, אף אחד מהמקורות הגרמנים המהימנים יותר לא טוען כך. פיתוחים מסוימים היו קרובים לניווט יחסי, במיוחד אלו הקשורים בהצבת גלאי על גירוסקופ, אבל בשום מקום לא ניתן למצוא הגדרה הדומה לזו שלעיל. התקדמות טכנולוגית לעבר יישום טכנולוגי של שיטת הניווט היחסי נעשתה במסגרת פיתוח הטיל מונחה תת אדום הראשון "Enzian" אשר יכל למדוד את קצב הסיבוב של קו הראייה למטרה באופן אוטומטי. המוטיבציה המרכזית לפיתוח אוטומציה כזאת הייתה תוצאות הניסויים המבצעיים בפצצות המונחות הראשונות שהיו מבוססות הנחיית מרדף (Pure Pursuit) - ניסויים הדגימו קשיים חמורים בהשגה מבצעית של פגיעה במטרה בשיטת הנחיה זו, במיוחד לקראת הפגיעה במטרה (Terminal Phase). כתוצאה, השיטה הרגילה של עקיבה אחר המטרה באמצעות מצלמת טלוויזיה המוצבת בקדמת הטיל ומשדרת למפעיל הפצצה תמונות של המטרה שזה בתורו משדר פקודות הנחיה מתאימות לפצצה - הייתה לא אפקטיבית ונוצר הצורך באוטומציה של התהליך.
בארצות הברית, המוטיבציה המרכזית לפיתוח טילי קרקע אוויר וטילי אוויר-אוויר מבוססי ניווט יחסי לקראת סיום המלחמה הייתה ללא ספק "מתקפות הקמיקאזה היעילות להחריד" נגד ספינות של צי ארצות הברית. היירוט המוצלח הראשון של טיל נגד כלי טיס (בלתי מאויש) היה בדצמבר 1950, על ידי הטיל "Lark" שפותח על ידי חברת ריית'יאון. באמצע שנות ה-50, הטילים מבוססי ניווט יחסי הראשונים הופיעו בכמה ארסנלים, וזה מפתיע שכמה מהם עדיין מיוצרים כיום יותר מ-40 שנה לאחר מכן, אף על פי שעם התאמות רבות ובעזרת שימוש בטכנולוגיות מודרניות.
יישום פשוט במונחי חומרה לניווט יחסי ניתן למצוא בטילי ה-AIM-9 סיידוויינדר המוקדמים. טילים אלו משתמשים במראה פרבולית הסובבת במהירות בתבנית אופיינית כגלאי. אלקטרוניקה פשוטה מאתרת את השגיאה הכיוונית שיש לגלאי עם המטרה (מקור קרינה אינפרה-אדומה), ומפעילה מומנט על המראה הגימבלית הזאת כדי לשמור על צירה מצביע על המטרה. מכיוון שהמראה היא למעשה גירוסקופ היא תמשיך להצביע על המטרה אם לא מופעל כח או מומנט חיצוני, ללא קשר לתנועות הטיל. במתח שהאלקטרוניקה מייצרת כדי להפעיל מומנט על המראה הדרוש כדי לנעול אותה על המטרה נעשה שימוש גם (כשהוא מוגבר) כדי להסיט את משטחי הניהוג שמנחים את הטיל, וכתוצאה משימוש כפול זה קצב הרוטציה של וקטור מהירות הטיל נעשה למעשה פרופורציונלי לקצב הרוטציה של קו הראייה.
לסיום, יש לציין כי טורפים בטבע הקדימו את בני האדם בשימוש בניווט יחסי:" [ניווט יחסי עם 1 < N] הוא קרוב לוודאי הדרך הפשוטה ביותר לפתור את הבעיה של ניווט. בעל חוליות הוא בעל מדי תאוצה שמאפשרים לו למדוד את קצב הפנייה שלו, בעוד שלטרף שלהם יש חיישנים דומים. כך המידע על קצב הפנייה של הטורף, המעובד ביחד עם המידע הכיווני מהעיניים, האוזניים והחושים האחרים במוח, מאפשר לצייד ליירט את הטרף שלו באופן יעיל ככל אפשר".
היתרון המרכזי של שיטת הניווט היחסי הוא שטיל שמתמרן לפיו ינוע במסלול "החלק" ביותר האפשרי, כלומר הוא יידרש לתמרן בצורה מזערית. לעקרון המזעור של התמרון יש שני היבטים חיוביים, האחד מתמטי והשני פיזיקלי. ההיבט המתמטי נוגע לעובדה שמבחינה פורמלית המסלול שמתקבל בניווט יחסי הוא אכן הטוב ביותר האפשרי, במובן שהוא הקרוב ביותר לקו ישר מבין כל המסלולים עם תנאי ההתחלה ותנאי הסיום הנתונים. ההיבט הפיזיקלי מתייחס לעובדה שלשאיפה למזעור התמרון יש הצדקה גם במנגנונים הפיזיקליים של הטיל; התמרון צורך אנרגיה חשמלית רבה הדרושה כדי להניע את הגאי הטיל כנגד עומס אווירודינמי גבוה מאוד. כדי להיווכח בנכונות ההיבט המתמטי, יש לפתח את הביטוי לאנרגיה של עקומה באמצעות הכלים של חשבון הווריאציות, ולהראות שהמסלול שמתקבל אכן ממזער את האנרגיה של העקומה. ניתן לפתח את הנוסחה לאנרגיה של עקומה באמצעות אנלוגיה פיזיקלית - נחשב את האנרגיה האצורה בקורה אלסטית בעלת צורה מסוימת הנתונה במאמץ אחיד כלשהו T. כידוע, הלחץ הרדיאלי שאלמנט אורך בעל אורך ds, רוחב w ועקמומיות C יוצר הוא: . לפיכך, האנרגיה שיש להשקיע כדי לקחת חתיכת קורה ישרה הנתונה במתיחות T ולעקם אותה לכדי קשת מעגלית בעלת עקמומיות C היא האינטגרל על הכוח הרדיאלי כאשר העקמומיות נעה מ-0 ל-C, שיחסי ל-: . לכן, האנרגיה של קורה אלסטית באורך s היא:
.
קורה אלסטית המקובעת בשני קצותיה ונתונה במאמץ אחיד תשאף למזער את האנרגיה שלה. ניתן לפתח את הביטוי לאנרגיה של עקומה גם בצורה מתמטית ישירה על בסיס משוואות אוילר-לגראנז'. באופן כללי יותר, האנרגיה של מסילה (לא בהכרח גיאודזית) ביריעה רימנית יחסית לאינטגרל של ריבוע העקמומיות הגיאודזית :
.
כלל הניווט היחסי (עם N = 3) ממזער את מאמץ הבקרה הנדרש מטיל, שהוא האינטגרל על תאוצת הטיל בריבוע - כאשר מהירות הטיל קבועה, אינטגרל זה למעשה שקול (עד כדי קבוע) לאינטגרל על עקמומיות המסלול בריבוע. לפיכך נוכחנו לדעת שכלל זה אכן ממזער את האנרגיה של עקומת המסלול.
ניווט יחסי כחוק הנחיה עם מאמץ בקרה מינימלי
עריכהנוכיח שניווט יחסי עם קבוע ניווט N = 3 ובמקרה של מטרה נייחת הוא אופטימלי מבחינת מאמץ הבקרה הנדרש, כלומר שהמסלול המתקבל מביא למינימום את אינטגרל הבקרה בריבוע. אינטגרל הבקרה בריבוע שווה למעשה למכפלת קבוע באינטגרל על עקמומיות המסלול בריבוע, ואינטגרל זה הוא גם גודל מתמטי מגאומטריה דיפרנציאלית המכונה האנרגיה של הפעולה של עקומה. כדי להוכיח זאת נעזר בקירוב של סמיכות למסלול התנגשות (NCC - Near Collision Course). לשם כך יש לחשב את ההשפעה של וריאציות מזעריות בפונקציית הבקרה לפי הזמן על פונקציונל מאמץ הבקרה. יש להוכיח שתחת וריאציה מזערית בבקרה שמקיימת שעדיין יש פגיעה במטרה שינוי אינטגרל הבקרה בריבוע הוא אפס. ברור שלשינויים קטנים בבקרה שמתרחשים בתחילת המסלול יש אפקט גדול יותר על הסטייה הסופית מהמטרה, באופן פרופורציונלי לזמן שנותר עד לסיום המסלול . לפיכך האינטגרלים על רכיבי הבקרה בציר x וציר Y צריכים לקיים: .
כאשר כש- היא זווית הרדיוס וקטור למטרה.
בנוסף, נגזרת אינטגרל הבקרה תחת וריאציה זו צריכה להיות שווה אפס:
ההנחה של וריאציה אינפיניטסימלית תבוא לידי ביטוי כעת בעובדה שנניח שהבקרה לזמן היא בקירוב זהה לזו שמתקבלת בניווט יחסי. נעזר בתוצאות מהפיתוח של המטרה הנייחת על התאוצה כתלות במרחק ובעובדה שזווית הפגיעה הסופית היא (תוצאה זו מתקבלת גאומטריה)ובעובדה ש- (כתוצאה מהקירוב של זוויות קטנות) ונקבל משילוב המשוואות:
. כעת נשים לב שאם נציב תוצאה זו לבקרה בתנאי שנגזרת אינטגרל הבקרה תחת הווריאציה שווה לאפס נקבל את התנאי הראשון כלומר נקבל:
וזהו זהותית התנאי שהווריאציה חייבת לקיים.
ניווט יחסי ומרחקי החטאה
עריכההרעיון הקונספטואלי מאחורי ניווט יחסי הוא לשאוף לנקודה מרוחקת אליה תגיע המטרה בעתיד, כלומר לשאוף למסלול התנגשות (Collision Course). במסלול התנגשות, קו הראייה נותר מקביל לעצמו במהלך תנועת המטרה והטיל, וניתן לשרטט משולש התנגשות (Collision Triangle) שאחד מקודקודיו הוא נקודת הפגיעה במטרה. כדי להבין את המשמעות המתמטית של חוק ההנחיה, נגדיר תחילה את מרחק ההחטאה (miss distance) כמרחק המינימלי שיהיה לטיל עם המטרה אם הוא ימשיך לנוע בקו ישר, ובמקרה של מטרה שלא מתמרנת, כלומר מטרה שנעה בקו ישר (Zero effort miss distance). נניח שמסלולי התנועה של המטרה והטיל קרובים למסלול התנגשות, כלומר שממערכת הייחוס של המטרה, הזווית בין מהירות הטיל (ששווה למהירות היחסית) לקו הראייה קטנה. נסמן זווית זו ב- .
מגאומטריה פשוטה נקבל שמרחק ההחטאה הוא: כש-r הוא המרחק הרגעי בין המטרה והטיל.
קצב הרוטציה של קו הראייה (LOS-rate) הוא: .
מהירות הסגירה מקיימת כי הזווית קטנה. לכן התאוצה שווה:
(הוא זמן המעוף הכולל של הטיל ).
קיבלנו שתאוצת הטיל יחסית למרחק ההחטאה! ויחסית הפוך לזמן המעוף בריבוע. תאוצת הטיל בניווט יחסי שואפת אם כן, להקטין את מרחק ההחטאה, וגודלה תלוי בזמן המעוף שנותר לטיל ויחסי למרחק ההחטאה.
מספר מקרים פרטיים חשובים של ניווט יחסי
עריכהמקרה 1: מטרה נייחת
עריכהנבחן את המקרה של טיל הנורה לעבר מטרה נייחת ומונחה בשיטת הניווט היחסי. במקרה זה, בשונה מהמקרה של הנחיית מרדף, זו אינה בעיה טרוויאלית. הסיבה לכך שטילים רבים שנורים לעבר מטרה נייחת מיישמים שיטת הנחיה זו חרף העלות הגבוהה של רכיבי הנחיית ניווט יחסי לעומת רכיבי הנחיית מרדף, היא היעדר דיוק מושלם ביריית הטיל לעבר מטרה מרוחקת. נניח שמשגר הטיל נמצא במרחק מהמטרה והטיל נורה בזווית ביחס לקו הראייה שמחבר בין מיקומו ההתחלתי של הטיל למטרה. כאשר היא הזווית בין קו הראייה למטרה לווקטור מהירות הטיל, היא הזווית שיוצר קו הראייה ביחס לקו הראייה ההתחלתי ו- הזווית שיוצר ווקטור מהירות הטיל, הקינמטיקה של הבעיה נתונה על ידי המשוואות הבאות:
כאשר מתקיים חוק ההנחיה . נחלק את המשוואה הראשונה בשנייה ונקבל:
. מחוק ההנחיה נובע שמתקיים ולכן: . מכאן נקבל על ידי אינטגרציה:
. תאוצת הטיל כתלות במרחק מהמטרה ניתנת על ידי : . ניתן לראות כי התאוצה היא אינסופית או אפס בנקודת הפגיעה אם או בהתאמה. זוהי מסקנה חשובה ביותר, למשל, בתכנון טילים נגד טנקים (הטנק איטי מאוד בהשוואה לטיל וניתן להתייחס אליו בקירוב כמטרה נייחת) - קבוע הניווט חייב להיות גדול או שווה 2 כדי לקבל תאוצות סבירות.
מקרה 2: מטרה נעה במהירות קבועה בקו ישר
עריכהלבעיה הכללית של ניווט יחסי אל מטרה שנעה במהירות קבועה בקו ישר לא קיים פתרון אנליטי פשוט. עם זאת קיים לה פתרון אנליטי במקרה הפרטי בו N = 2. נפתח אותו כאן.
נכתוב את משוואות התנועה בקואורדינטות פולריות ממערכת הייחוס של המטרה, כלומר נכתוב את מיקום הטיל בקואורדינטות . כמו מקודם בדוגמה עם המטרה הנייחת מתקיים שהזווית של מהירות הטיל עם הרדיוס וקטור היא (בהנחה שבתחילה מהירות הטיל היא בכיוון הרדיוס וקטור). לפיכך מתקיים מגאומטריה שקצב ההתקרבות הרגעי של הטיל והמטרה הוא:
. כמו כן קצב הסיבוב של קו הראייה הוא:
.
נחלק את המשוואות זו בזו ונקבל:
או:
כאשר . מכאן נקבל:
.
מכיוון ש-N - 1 = 1 ניתן לסמן ולקבל שהאינטגרל שווה:
או:
והיירוט מתרחש בזווית פגיעה סופית שמקיימת:
.
יישום טכנולוגי של ניווט יחסי
עריכהפוטוקונדוקטיביות
עריכהבשנות ה-20 נתגלה, כי חשיפת חומרים מסוימים וביניהם סולפיד לקרינה תרמית תת-אדומה מפחיתה באופן משמעותי את ההתנגדות החשמלית של החומר. זוהי דוגמה של תכונה הנקראת "פוטוקונדוקטיביות" (Photoconductivity). תכונה זו מאפשרת להעביר אותות חשמליים בחומר בתגובה לחשיפה קצרה לאור בתדר מתאים. באמצעות תכונה זו ניתן למדוד את הזרם הנוצר ולקשר בין תוצאת המדידה לפעולה מסוימת המחוללת אותה. התגלית הצמיחה מגוון המצאות ויישומים צבאיים, מהנחיית טילים מבוססת תת-אדום למערכות ראיית לילה.
ראש הביות
עריכהכדי למדוד את קצב הסיבוב של קו הראייה למטרה, יש לסרוק את המרחב מסביב לטיל ולמדוד פעמיים את מיקומה הזוויתי של המטרה (מקור קרינת חום) יחסית לציר הראשי של הטיל. ראש ביות טיפוסי מורכב, כמוראה באיור, ממראה מלבנית מסתובבת במהירות גבוהה מאוד כשמלפנים לה מוצב גלאי עשוי מחומר מתאים. אלומת הקרינה התת-אדומה מגיעה מכיוון מסוים ולפיכך המראה תחזיר "הבזק" תת-אדום קצר כאשר היא תהיה באזימוט המתאים (זווית w1 באיור) ביחס לציר הטיל. מכיוון שהמראה מסתובבת במהירות קבועה, מדידת הזמן שבו מתקבל הבזק מאפשרת לדעת את האזימוט הרגעי של המטרה ומדידת משך הזמן שבין שני הבזקים עוקבים מאפשרת לקבוע את קצב שינוי האזימוט של המטרה.
מדידת ההגבהה (זווית w2 באיור) מורכבת יותר ומתבססת על הרעיון שככל המטרה רחוקה יותר מציר הטיל היא תפיק הבזק קצר יותר שכן המהירות הליניארית של המראה גבוהה יותר בקצוות מאשר במרכז. המידע על שינוי האזימוט וההגבהה מעובד במערכת הבקרה של הטיל לפקודות בקרה מתאימות להגאי הטיל באופן שמשקלל את קבוע הניווט הרצוי מההנחיה וכך מונחה הטיל אל מטרתו.


