מעגל (תורת הגרפים)

בתורת הגרפים, מעגל (באנגלית: Cycle graph או Circular graph) הוא גרף המורכב ממסלול לא-ריק המתחיל ומסתיים באותו צומת, כאשר הצמתים היחידים שחוזרים על עצמם הם הצומת הראשון והצומת האחרון.

מעגל

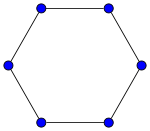גרף מעגל פשוט באורך 6
מספר צמתים	n
מספר קשתות	n
אוטומורפיזם	(2n (Dn
מספר צבעי צומת	2 (גרף זוגי) 3 (אי זוגי)
מספר צבעי קשת	2 (גרף זוגי) 3 (אי זוגי)
תכונות	גרף קשיר גרף רגולרי מסלול אוילרי מסלול המילטוני גרף דו-צדדי
סימון	Cn

באופן פורמלי, מעגל הוא גרף בעל צמתים $\ v_{0},\dots ,v_{n-1}$, עם הקשתות $\ v_{i},v_{i+1{\pmod {n}}}$.

נהוג לסמן גרף מעגל המורכב מ-$\ n$ קשתות כך: C_n. בגרף C_n מספר הקשתות שווה למספר הצמתים (שווה ל-$\ n$) ודרגת כל צומת שווה ל-2. כלומר, מכל צומת יוצאות שתי קשתות.

טרמינולוגיה

ישנם שמות נרדפים רבים לגרף מעגל: גרף מעגל פשוט (simple cycle graph), גרף מעגלי (cyclic graph), על אף שהשם השני אינו שכיח כיוון שהוא עשוי להתייחס גם למקרה הכללי יותר שבו הגרף מכיל מעגלים (כלומר, אינו גרף חסר מעגלים (acyclic graph)). שמות נפוצים נוספים: מעגל, פוליגון, n-gon.

מעגל בעל מספר זוגי של צמתים נקרא מעגל זוגי (even cycle); מעגל בעל מספר אי-זוגי של צמתים נקרא מעגל אי-זוגי (odd cycle).

תכונות

• הגרף הוא גרף קשיר
• הגרף הוא גרף 2-רגולרי
• הגרף הוא בעל מסלול אוילרי
• הגרף הוא בעל מסלול המילטוני
• הגרף הוא גרף 2-צביע - אם ורק אם יש מספר זוגי של צמתים
• הגרף הוא גרף 3-צביע
• הגרף הוא גרף דו-צדדי - אם ורק אם יש מספר זוגי של צמתים

גרף מעגל מכוון

גרף מעגל מכוון שאורכו 8

גרף מעגל מכוון הוא סוג של גרף מכוון שהוא גם גרף מעגל. שכל הקשתות בו מופנות לאותו כיוון.

הוצאת קבוצת הצמתים המינימלית שתהפוך את הגרף לחסר מעגלים שווה ל-1. תהליך זה נקרא feedback vertex set. הוצאת קבוצת הקשתות המינימלית שתהפוך את הגרף לחסר מעגלים שווה ל-1. תהליך זה נקרא feedback arc set.

בגרף זה, דרגת הכניסה שווה ל-1 ודרגת היציאה שווה ל-1.

דרכים למציאת מעגלים בגרפים

1. עקרון שובך היונים: כל מסלול בגרף באורך n+1 קודקודים מכיל מעגל.
2. קיימים 2 או יותר עצים פורשים לגרפים: אין גרף שיש לו יותר מ-2 עצים פורשים, אם יש יותר מעץ פורש אחד אז מדובר במעגל, עבור K עצים פורשים ניתן לצייר מעגל בעל K צמתים.
3. הרצת אלגוריתם DFS: במהלך הרצת האלגוריתם כל קשת אחורה שאינה בעץ הפורש היא מעגל.

ראו גם

• גרף שלם

קישורים חיצוניים

מדיה וקבצים בנושא מעגל בוויקישיתוף

• מעגל, באתר MathWorld (באנגלית)