קיוביט
המונח קיוביט (אנגלית: Qubit; סיבית קוונטית) משמש כיחידת מידה למידע קוונטי, וגם לתיאור אלמנט אחסון המידע הקטן ביותר במחשב קוונטי. זהו האנלוג הקוונטי של הביט בתורת המידע הקלאסית. במחשב קוונטי, קיוביט הוא מערכת קוונטית בעלת שני מצבים.

בערך זה |
ייצוג מתמטי של קיוביט
עריכהקיוביט ניתן לרישום מתמטי בתור וקטור במרחב הילברט[1] דו-ממדי. על פי רוב מסמנים את מצבי הבסיס של הקיוביט כ- ו- , או כ- ו- , בהתאמה. סימון נפוץ נוסף הוא ו- , הקרוי בסיס הדמר. בסימון דיראק ניתן ליצג קיוביט כללי באופן הבא: , כאשר , ומתקיים . באופן ויזואלי ניתן לחשוב על קיוביט כללי ביותר כעל נקודה על פני כדור היחידה (כדור ברדיוס אחד). כדור זה הקרוי לרוב כדור בלוך או "ספירת בלוך" על שם הפיזיקאי פליקס בלוך.
מימוש פיזיקלי של קיוביט
עריכהקיימות מספר מערכות פיזיקליות המממשות קיוביט:
- חלקיק כלשהו (למשל אלקטרון או אטום). כאשר כיוון הספין בהטלה על ציר מסוים מתאר מערכת שני מצבים.
- פוטון. הרמות השונות יכולות להיות למשל קיטוב שונה של הפוטון, זמן ההגעה של הפוטון, או כמות הפוטונים בפולס אור.
מכיוון שההנדסה של מערכות כאלו היא לא פשוטה, קיוביטים נבנים לעיתים קרובות מערכות שניתן להתייחס עליהן כמערכות שתי רמות רק בקירוב. לדוגמה, בקיוביטים על מוליכים, נעשה שימוש באוסילטור לא הרמוני, שהפרש הרמות שלו לא אחיד. מכיוון שיש הפרש אנרגיה ספציפי בין כל שתי רמות, ניתן לעורר בדיוק רב רק את זוג הרמות הראשונות, ולהתייחס אליהן כקיוביט.
קיוביט מול ביט
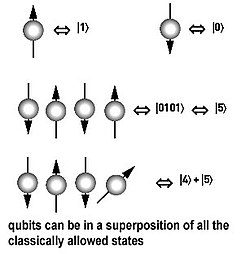
עריכהבניגוד לביט קלאסי, שיכול להיות באחד משני המצבים 0 או 1, קיוביט הוא מערכת שני מצבים קוונטית ולכן יכול להיות במצב 0, 1, או בסופרפוזיציה קוונטית של מצבים, ועשוי להיות שזור עם קיוביטים אחרים.
בעוד שלביט קלאסי ישנם שני ערכים אפשריים בלבד, 0 או 1, מדידה קוונטית היא תהליך הסתברותי, ותוצאתה תלויה בבסיס המדידה. לאחר ביצוע מדידה קוונטית מצבו של הקיוביט נהרס בתהליך שמכונה קריסת פונקציית גל, ונותרת תשובה קלאסית לחלוטין - אילו מבין שני מצבי הבסיס של הקיוביט נמדדו. מדידה של שכפולים רבים של אותו קיוביט תיתן תוצאה הסתברותית בהתאם למצב הקוונטי שבו הקיוביט נמצא.
כאשר מבצעים מדידה בבסיס נתון (נניח, ו- , המכונה בסיס החישוב) המקדמים של אברי הבסיס הנ"ל מתארים את ההסתברות למדוד את אותו איבר-בסיס. לדוגמה, אם נמדוד קיוביט שהוא בסופרפוזיציה מאוזנת של מצבי הבסיס ו , כלומר את הקיוביט מהצורה , נקבל בחצי מהפעמים את התוצאה ובחצי את התוצאה . באופן כללי, מדידה בבסיס החישוב של המצב תתן את התוצאה בהסתברות ואת התוצאה בהסתברות .
הרחבות של קיוביט
עריכהניתן להרחיב את מושג הקיוביט ממערכת דו-ממדית, למערכת תלת-ממדית (קיוטריט, qutrit), או מערכת d-ממדית (קיודיט, qudit). במובן הרחב, ניתן להרחיב את המצב הקוונטי למערכת בעלת ממד אינסופי. למשל, פולס של אור יכול להכיל (באופן תאורטי) מספר כלשהו של פוטונים. אם נסמן ב- מצב קוונטי המתאים לפולס אור המכיל פוטונים, נוכל לתאר פולס כללי ביותר, שהוא סופרפוזיציה של מספר כלשהו של פוטונים בצורה הבאה
מדידה
עריכהמדידה מלאה של קיוביט (מעל בסיס נתון) היא תהליך המקבל כקלט מצב קוונטי של קיוביט, ומחזיר כפלט אינדקס (מספר קלאסי). המדידה היא תהליך הסתברותי, בה ככל שהמצב הקוונטי שנמדד קרוב יותר לאחד מאברי הבסיס, גדלה ההסתברות לקבל את האינדקס המתאים לאותו אבר.
לדוגמה, ביצוע מדידה בבסיס החישוב, תחזיר את האינדקס 0 כאשר "נמדד" המצב ואת האינדקס 1 כאשר נמדד . במקרה בו הקיוביט הנמדד נמצא בסופרפוזיציה של אברי הבסיס, ההסתברות למדוד כל אבר בסיס היא ריבוע המקדם של אותו אבר בסופרפוזיציה. למשל, מדידת המצב בבסיס החישוב, תיתן את התוצאה 0 בהסתברות חצי ואת התוצאה 1 בהסתברות חצי, מכיוון שמצב זה הוא סופרפוזיציה מאוזנת של אברי בסיס החישוב, .
באופן פורמלי, מדידה של קיוביט כלשהו , מעל בסיס נתון , היא פונקציה הסתברותית בה ההסתברות לקבל במדידה את הערך i, נתונה לפי , כאשר הוא מקדם אבר הבסיס ברישום הקיוביט לפי הבסיס הנתון . מתקיים גם .
באופן דומה, מדידה של n קיוביטים במצב מעל בסיס נתון היא פונקציה הסתברותית בה ההסתברות לקבל את האינדקס נתונה על ידי .
מדידה מלאה אינה המדידה הכללית ביותר המתאפשרת על ידי תורת הקוונטים, אך קיימת הוכחה כי ניתן לבצע כל מדידה כללית ביותר על ידי הוספת קיוביטים, הפעלת טרנספורמציה יוניטרית על האוגר המורחב, וביצוע מדידה מלאה לאוגר זה [2].
ראו גם
עריכהקישורים חיצוניים
עריכה- אשכול מחשוב קוונטי באתר הידען.
- עקרונות בסיסיים בחישוב קוונטי, מתוך אתר Quantiki - אתר wiki המוקדש לחישוב קוונטי.
- קיוביט, באתר MathWorld (באנגלית)
הערות שוליים
עריכה- ^ באופן מפורש, נדון במרחב עם המכפלה הפנימית:
- ^ John Preskill. Lecture notes for Physics 229: Quantum information and computation, 1998.