התפלגות בטא

בתורת ההסתברות ובסטטיסטיקה, התפלגות בטא היא משפחה של התפלגויות רציפות, המוגדרות על הקטע [0,1] ובעלות שני פרמטרים המשפיעים על צורת ההתפלגות: α ו-β. קבוע הנרמול של פונקציית צפיפות ההסתברות הוא פונקציית בטא של הפרמטרים, ומכאן שמה של ההתפלגות.

התפלגות בטא

פונקציית צפיפות ההסתברות
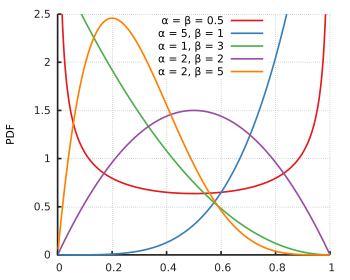פונקציית ההסתברות המצטברת
מאפיינים
פרמטרים	α > 0 β > 0
תומך	$x\in [0,1]$ או $x\in (0,1)$

להתפלגות בטא תפקידים רבים בבחינת התנהגות של משתנים מקריים המוגבלים למרווחים סופיים בדיסציפלינות רבות. הרחבה של ההתפלגות נקראת התפלגות דיריכלה, על שמו של המתמטיקאי הגרמני-צרפתי יוהאן דיריכלה.

מאפיינים

פונקציית הצפיפות

עבור $0\leq x\leq 1$ ועבור הפרמטרים $\alpha ,\beta >0$, פונקציית הצפיפות של ההתפלגות מוגדרת כך:

${\begin{aligned}f(x;\alpha ,\beta )&={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\displaystyle \int _{0}^{1}u^{\alpha -1}(1-u)^{\beta -1}\,du}}\\[6pt]&={\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\\[6pt]&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}x^{\alpha -1}(1-x)^{\beta -1}\end{aligned}}$

כאשר $\Gamma (z)$ היא פונקציית גמא ו-B היא פונקציית בטא.

פונקציית הצפיפות המצטברת

פונקציית הצפיפות המצטברת מוגדרת על ידי הנוסחה:

$F(x;\alpha ,\beta )={\dfrac {\mathrm {B} {}(x;\alpha ,\beta )}{\mathrm {B} {}(\alpha ,\beta )}}=I_{x}(\alpha ,\beta )$

כאשר $\mathrm {B} (x;\alpha ,\beta )$ היא פונקציית הבטא הלא שלמה.

התוחלת

התוחלת של ההתפלגות היא פונקציה של היחס β/α:

${\begin{aligned}\mu =\operatorname {E} [X]&=\int _{0}^{1}xf(x;\alpha ,\beta )\,dx\\&=\int _{0}^{1}x\,{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}\,dx\\&={\frac {\alpha }{\alpha +\beta }}\\&={\frac {1}{1+{\frac {\beta }{\alpha }}}}\end{aligned}}$

כאשר הפרמטרים שווים, התוחלת שווה ל-1/2, מה שאומר כי במקרה זה ההתפלגות היא סימטרית והתוחלת היא מרכז התפלגות.

השונות

השונות של ההתפלגות מוגדרת כך:

$\operatorname {var} (X)=\operatorname {E} [(X-\mu )^{2}]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}$

כאשר $\alpha =\beta$, השונות היא:

$\operatorname {var} (X)={\frac {1}{4(2\alpha +1)}},$

ראו גם

• התפלגות בטא-בינומית

קישורים חיצוניים

מדיה וקבצים בנושא התפלגות בטא בוויקישיתוף

• התפלגות בטא, באתר MathWorld (באנגלית)