התפלגות גאומטרית
בתורת ההסתברות ובסטטיסטיקה, ההתפלגות הגאומטרית היא אחת משתי התפלגויות ההסתברות הבדידות הבאות:
- התפלגות ההסתברות של – מספר ניסויי ברנולי הנדרשים עד להשגת הצלחה אחת. נע בטווח .
- התפלגות ההסתברות של – מספר הכשלונות בניסויי ברנולי לפני ההצלחה הראשונה. נע בטווח .
| פונקציית ההסתברות | |
 | |
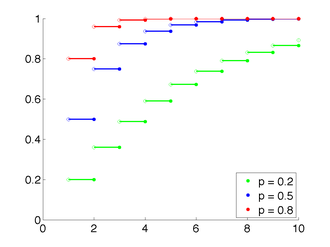
| פונקציית ההסתברות המצטברת | |
|---|---|
 | |
| מאפיינים | |
| פרמטרים | (ההסתברות להצלחה) |
| תומך | |
|
פונקציית הסתברות (pmf) | |
|
פונקציית ההסתברות המצטברת (cdf) | |
| תוחלת | |
| סטיית תקן | |
| חציון | (לא יחיד אם הוא מספר שלם) |
| ערך שכיח | |
| שונות | |
| אנטרופיה | |
|
פונקציה יוצרת מומנטים (mgf) | |
| פונקציה אופיינית | |
| צידוד | |
| גבנוניות | |
כיצד נקבע מי משתי התפלגויות אלו מכונה ההתפלגות הגאומטרית הוא עניין של מוסכמה ונוחות, בהתאם להקשר.
אם ההסתברות להצלחה בכל ניסיון היא , אז ההסתברות ש- ניסיונות נדרשים עד להשגת ההצלחה הראשונה היא:
בצורה דומה, ההסתברות שיהיו כישלונות לפני ההצלחה הראשונה היא:
בשני המקרים, סדרת ההסתברויות היא סדרה גאומטרית, ומכאן שמה של ההסתברות.
לדוגמה, נניח כי קוביית משחק רגילה מוטלת שוב ושוב עד הפעם הראשונה בה מופיע המספר 1. התפלגות מספר זריקות הקוביה היא התפלגות גאומטרית עם הפרמטר .
צורת ההתפלגות
עריכהככל ש עולה, ההתפלגות נעשית מרוכזת יותר סביב הממוצע, עם פחות ערכים קיצוניים. ככל ש יורד, ההתפלגות נעשית מפוזרת ושטוחה יותר, עם ערכים קיצוניים יותר.
ככל ש עולה, ההתפלגות הופכת מפוזרת יותר, עם ערכים קיצוניים יותר. כאשר יורד, ההתפלגות נעשית מרוכזת יותר סביב הממוצע, עם פחות ערכים קיצוניים.
כאשר שואף לאפס ההתפלגות שואפת להתפלגות בינומית שלילית. כאשר כאשר שואף ל-1 ההתפלגות שואפת להתפלגות היחידה.
במקרה (כלומר, יש רק כישלון אחד לפני ההצלחה הראשונה) נקבל את ההתפלגות הבינומית השלילית עם .
תכונות
עריכה- חוסר זיכרון. לאחר כישלונות הסיכוי להצלחה בניסיון ה- , שווה לסיכוי להצלחה בניסיון ה- : .
- הסיכוי שההצלחה הראשונית תקרה לאחר n ניסיונות הוא הסתברות ל- כישלונות רצופים: .
- התוחלת והשונות של מספר הניסיונות עד להצלחה כולל:
- התוחלת והשונות של מספר הכשלונות עד להצלחה:
- מדגימה את מספר ניסויי ברנולי (כלומר, ניסויים עצמאיים עם שתי תוצאות אפשריות בלבד) הנדרשים כדי להשיג הצלחה בודדת.
ראו גם
עריכהקישורים חיצוניים
עריכה- התפלגות גאומטרית, באתר MathWorld (באנגלית)
























