גאומטריה פרויקטיבית
גאומטריה פרויקטיבית היא גאומטריה לא אוקלידית, שבה אקסיומת המקבילים מוחלפת באקסיומה אחרת: כל שני ישרים במישור נפגשים בנקודה.
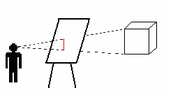
באיור שמשמאל מתוארות הנחות היסוד לציור בפרספקטיבה. הצייר ניצב מול בד ציור, ומצייר את הנראה לו מאחורי הבד. כדי לצייר עצם בעולם, יש למתוח קו ישר מהעצם אל עין הצייר, ולחתוך את הקו ישר עם מישור הבד. נקודת חיתוך זו, הנקראת נקודת המגוז, היא המקום על הבד בו צריכה להיות מצוירת הנקודה המקורית. בגישה זו אין התייחסות להשפעה של שתי העיניים על הראייה.

צייר הניצב מול מושא הציור שלו יכול, כמובן, לצייר בדיוק יחסי גם בלא צורך בתאוריה מתמטית מורכבת. הצייר יכול, למשל, למדוד בעין מרחקים במושא הציור שלו בעזרת סרגל המוחזק בידו הפשוטה קדימה, ולהעתיק מרחקים אלו אל הדף. עם זאת, ציירי הרנסאנס ציירו תכופות את התמונות מדמיונם. בפרסקו של מזאצ'ו "השילוש הקדוש" (משמאל) מתואר ישו הצלוב בחזיתו של מבנה בעל עיצוב מורכב (קמרון חבית שתקרתו מרוצפת בתיבות). על מנת לצייר מבנה כגון זה בדיוק הנדרש היה על הצייר (כפי הנראה) לשרטט מראש מבנה כזה בתרשימי צד ובסיס. לאחר מכן בנה הצייר תמונה של המבנה התלת-ממדי, בעזרת התרשימים הנ"ל, על ידי חישובים מתמטיים.
תולדות הענף
עריכההגאומטריה הפרויקטיבית נולדה מתוך הצרכים המעשיים של אמני הציור. בימי הביניים היה הציור רוחני וסמלי. לקראת הרנסאנס עלתה קרנו של הציור המדויק – הדומה לנראה בעין. החייאת הכתבים הקלאסיים והאמונה שבבסיס הטבע עומדים עקרונות מתמטיים, הובילה את הציירים והמתמטיקאים בני התקופה לנסות ולמצוא שיטה סדורה לציור העולם התלת-ממדי על בד ציור דו-ממדי.
האמנים הראשונים בתחום זה שמשנתם ידועה לנו היו פיליפו ברונלסקי ולאונה בטיסטה אלברטי, שחיבר את הטקסט הראשון (הידוע כיום) בנושא, שכותרתו "על הציור" – De pictura. אנשי מפתח מאוחרים יותר בתחום זה הם פיירו דלה פרנצ'סקה, לאונרדו דה וינצ'י, אלברכט דירר ואחרים.
המתמטיקאי ז'ראר דזארג (Gérard Desargues) היה ממניחי היסודות התאורטיים לגאומטריה הפרויקטיבית, ועסק בה יחד עם בלז פסקל. באחד מחיבוריו מתאר דזרג מתכון שלם לציור עצם בפרספקטיבה מנקודת מבט מסוימת, מתוך תרשימי הבסיס והצד שלו. הענף נזנח במשך כמאתיים שנים, בין היתר עקב ההתפתחויות המטאוריות של הגאומטריה האנליטית והחשבון האינפיניטסימלי באותה התקופה. כתביהם של דזרג ושל פסקל אבדו. ז'אן-ויקטור פונסלה (Jean-Victor Poncelet) נחשב למחיה הגאומטריה הפרויקטיבית. הוא שרת כקצין בצבא נפוליאון, ונפל בשבי בזמן הפלישה לרוסיה. בזמן שהותו בשבי, בשנים 1813–1814, שחזר פונסלה את אשר למד בתחום הגאומטריה ממורו גספאר מוֹנז' (Gaspard Monge), והצליח לפתח תוצאות חדשות בגאומטריה פרויקטיבית. מחקריו של פונסלה הובילו לחקר מחדש של הנושא, וממשיכיו העמיקו חקר מעבר לתוצאות של דזרג ופסקל.
בשנת 1845 נתקל המתמטיקאי הצרפתי מישֵל שָל (Michel Chales) בעותק שכוח בכתב יד של מאמר של דזרג בנושא (שעסק בחתכי חרוט). כך נודע היקף עבודתו של דזרג בנושא. בזמן זה שוחזרו כבר רוב תוצאותיו של דזרג בידי מתמטיקאים בני התקופה. באותה עת תרמו לגאומטריה הפרויקטיבית גם יעקב שטיינר, לואיג' קרמונה וארתור קיילי. גישתו של פליקס קליין לגאומטריה דרך סימטריות חיברה את הגאומטריה הפרויקטיבית לאלגברה. בסוף המאה ה-19 ותחילת המאה ה-20 תרמו לתחום גם דויד הילברט, אוסוולד ובלן וג'ון וסלי יאנג (אנ'), שפיתחו את הגישה האקסיומטית.
הגישה האקסיומטית
עריכהגישתו של אוקלידס, ב"יסודות", הייתה לתאר את המבנה המורכב של הגאומטריה האוקלידית באמצעות אקסיומות. באופן דומה אפשר לתת גם למישור הפרויקטיבי הגדרה אקסיומטית.
מנקודת מבט מודרנית, פירושו של דבר הוא שמערכת מתמטית הכוללת "נקודות" ו"ישרים", עם יחס חילה (הקובע אילו נקודות "נמצאות על" אילו ישרים), נקראת מישור פרויקטיבי, אם היא מקיימת את חמש האקסיומות הבאות:
- יש לפחות ישר אחד.
- דרך כל שתי נקודות שונות עובר ישר יחיד.
- כל שני ישרים נחתכים לפחות בנקודה אחת.
- על כל ישר יש לפחות שלוש נקודות שונות.
- אין ישר אשר כל הנקודות נמצאות עליו.
האקסיומה הראשונה והחמישית מונעות קבלת מערכות פתולוגיות (כגון: מישור שאין בו נקודות וישרים כלל, או מישור שיש בו ישר אחד בלבד) כמישורים פרויקטיביים. למעשה, במישור הפרויקטיבי הקטן ביותר יש שבע נקודות ושבעה ישרים (זהו המישור הפרויקטיבי מעל השדה בן שני איברים, ראו להלן).
באמצעות האקסיומות שמקיים מישור פרויקטיבי ניתן להוכיח את הטענות הבאות:
- כל שני ישרים שונים נחתכים בדיוק בנקודה אחת.
- דרך כל נקודה עוברים לפחות שלושה ישרים שונים.
- אין נקודה אשר כל הישרים עוברים דרכה.
ניתן לתאר גם מרחבים פרויקטיביים תלת-ממדיים (או יותר) באופן אקסיומטי, אלא שהדבר דורש אקסיומות נוספות לקביעת היחס בין ישרים שאינם שייכים לאותו מישור.
עקרון הדואליות
עריכההדואליות בגאומטריה פרויקטיבית מתייחסת להחלפה של נקודות וישרים, תוך שמירה על יחס החילה (נקודה על ישר הופכת לישר שעליו נקודה). המבנה הדואלי לישר שעליו ארבע נקודות הוא נקודה שדרכה עוברים ארבעה ישרים, וכן הלאה. לדוגמה, אם נגדיר "משולש" כשלשה של נקודות שאינן על ישר אחד עם הישרים העוברים דרכן, נגלה שהמבנה הדואלי כולל שלושה ישרים שאינם נפגשים בנקודה, עם נקודות החיתוך שלהם - דהיינו, משולש. כלומר המשולש דואלי למשולש.
חשיבותה של הדואליות בגאומטריה פרויקטיבית נובעת מכך שמערכת האקסיומות (יחד עם שלוש הטענות שנוסחו לעיל) היא דואלית. הווה אומר, אם נחליף את כל הישרים בנקודות, ואת הנקודות בישרים, נקבל סידור מחדש של שמונה הפסוקים. משתמע מכך, שהמושגים נקודה וישר הם דואליים בגאומטריה פרויקטיבית. מכאן נובע שלכל משפט שניתן להוכיח בגאומטריה פרויקטיבית, נכון גם המשפט הדואלי (המתקבל מהחלפת ישרים ונקודות).
מרחבים פרויקטיביים
עריכה- ערך מורחב – מרחב פרויקטיבי
מרחב פרויקטיבי הוא מרחב המקיים את האקסיומות של הגאומטריה הפרויקטיבית. המרחב הפרויקטיבי דומה למרחב האוקלידי, אולם כל שני ישרים נפגשים בו בנקודה. כלומר, הוא אינו מקיים את האקסיומה החמישית של אוקלידס. המרחב הפרויקטיבי הממשי ה-n-ממדי דומה למרחב האוקלידי ה-n-ממדי, בתוספת של "נקודות אינסוף". נקודות אלו נוספות לכל כיוון במרחב, וכל שני ישרים בעלי אותו כיוון יחתכו בנקודת האינסוף של הכיוון.
העתקות פרויקטיביות
עריכה- ערך מורחב – העתקה פרויקטיבית
העתקה פרויקטיבית היא העתקה במרחב פרויקטיבי שהיא הרכבה של מספר הטלות פרספקטיביות (ראו העתקה פרויקטיבית). אינטואיבית, ההעתקה הפרויקטיבית תעביר בין ייצוגים שונים של קבוצות נקודות, מנקודת מבט שונה. כלומר, ההעתקה תעביר בין הטלות שונות של עצם, המבוצעות מנקודות מבט שונות על טווחים שונים.
בהינתן מרחב פרויקטיבי P שנבנה מתוך מרחב וקטורי V, ההעתקות הפרויקטיביות על P תושרינה מתוך קבוצת ההעתקות הליניאריות על V.
ידוע כי בהינתן שתי n-יות של וקטורים בלתי-תלויים במרחב וקטורי V ישנה העתקה ליניארית יחידה המעבירה ביניהם. המשפט היסודי של הגאומטריה הפרויקטיבית טוען כי בהינתן שתי n-יות של נקודות במצב כללי ב-P ישנה העתקה פרויקטיבית יחידה המעבירה ביניהן. הוכחת המשפט נובעת באופן ישיר יחסית מהוכחת המשפט המקביל במרחב הווקטורי.
העתקה פרויקטיבית כללית אינה משמרת אורכים, זוויות או מקבילות. מאידך גיסא היא מעתיקה ישרים לישרים ונקודות לנקודות, ומשמרת חילה של ישרים בנקודות. גודל נוסף הנשמר על ידי ההעתקה הוא היחס הכפול שיפורט להלן.
משפטים מרכזיים
עריכהמשפט דזרג קובע שאם שני משולשים פרספקטיבים ביחס לנקודה, אז הם פרספקטיבים גם ביחס לישר. המשפט הזה חל בכל מרחב פרויקטיבי מממד 3 או יותר, אבל הוא אינו מתקיים בכל מישור פרויקטיבי.
משפט פאפוס: בהינתן זוג ישרים הנחתכים ב-O. וכן תהינה הנקודות , כשכל הנקודות שונות מ-O. אזי, שלושת החיתוכים , , , הם על ישר אחד.
גם משפט פאפוס אינו נובע מהאקסיומות של הגאומטריה הפרויקטיבית. יתרה מזאת, משפט פאפוס אינו נובע גם משילובם של משפט דזרג והאקסיומות, אך לפי משפט של גרהרד הסנברג[1], ניתן להוכיח את משפט דזרג באמצעות משפט פאפוס.
יחס כפול
עריכה- ערך מורחב – יחס כפול
במשך תקופה ארוכה המתמטיקאים חפשו אחר שמורות של העתקות פרויקטיביות במישור. לפי המשפט היסודי של הגאומטריה הפרויקטיבית, קיימת העתקה פרויקטיבית (יחידה) המעבירה בין שתי שלשות נתונות של נקודות שאינן על ישר. לכן, לא תתכנה שמורות כאלה בקבוצות של שלוש נקודות, והן תופענה בקבוצות של ארבע נקודות לפחות.
בהינתן ישר פרויקטיבי, תהינה ארבע נקודות, כש- הן שונות. מהמשפט היסודי של הגאומטריה הפרויקטיבית ידוע כי ישנה העתקה יחידה המקימת , ו- . נטען שהגודל נשמר תחת העתקות פרויקטיביות. גודל זה נקרא היחס הכפול של רביעיית הנקודות, ומסומן .
תהינה ארבע נקודות המקימות כי ההעתקה מעבירה את הרביעייה הראשונה לרביעייה השנייה. עלינו להראות כי . ההרכבה מקיימת , ו- . מהגדרת היחס הכפול ידוע , אולם וכך היחס הכפול של הרביעיות זהה.
ליחס הכפול ישנה משמעות גאומטרית. כאמור, העתקות פרויקטיביות אינן משמרות ארכי ישרים, ואף היחס בין אורכים שונים אינו נשמר, שכן זוויות אינן נשמרות. היחס הכפול של רביעיית נקודות הוא למעשה היחס בין היחסים של האורכים של ששת הקטעים שבין ארבע הנקודות הנ"ל. ביטוי מפורש ליחס הכפול נתן למצוא בערך עליו.
חתכי חרוט במרחב פרויקטיבי
עריכהאת חתכי החרוט ב- ניתן למיין לשמונה מחלקות שונות:
- קבוצה ריקה.
- נקודה בודדת.
- ישר.
- זוג ישרים מקבילים.
- זוג ישרים נחתכים.
- אליפסה / מעגל.
- היפרבולה.
- פרבולה.
המחלקות הנ"ל נשמרות תחת העתקות ליניאריות והזזות.
אם נמיין את השניוניות במישור הפרויקטיבי נקבל חמש מחלקות בלבד:
- קבוצה ריקה.
- נקודה.
- ישר.
- זוג ישרים כלשהו.
- אליפסה / מעגל, היפרבולה ופרבולה.
הפעם המחלקות נשמרות תחת העתקות פרויקטיביות.
- ניתן לעבור בין זוג ישרים מקבילים ובין זוג ישרים נחתכים. זאת מכיוון שגם זוג ישרים מקבילים נחתך במישור הפרויקטיבי בנקודת האינסוף. לכן, העתקה פרויקטיבית המעבירה נקודה סופית כלשהי לנקודת אינסוף כלשהי, תעביר זוג ישרים הנחתכים בנקודה הסופית לזוג ישרים מקבילים, וכן בכיוון השני.
- ניתן להעביר אליפסה במישור הפרויקטיבי לפרבולה או להיפרבולה. כל העתקה פרויקטיבית מעבירה בין ישרים. בפרט, ישנו ישר כלשהו המועתק לישר האינסוף במישור הפרויקטיבי. אם ישר זה משיק לאליפסה, נקודת ההשקה שעליו תעבור לנקודת אינסוף כלשהי, וכך האליפסה תועתק לפרבולה. באופן דומה, אם ישר זה חותך את האליפסה, שתי נקודות החתוך שעליו תועברנה לשתי נקודות אינסוף, ובכך תתקבל היפרבולה.
ראו גם
עריכהקישורים חיצוניים
עריכה- גאומטריה פרויקטיבית, באתר MathWorld (באנגלית)
- טל הסנר, על הגיאומטריה, הפרספקטיבה והעולם שאנו רואים, אודיסאה 17, אוקטובר 2012
- גאומטריה פרויקטיבית, באתר אנציקלופדיה בריטניקה (באנגלית)
- גאומטריה פרויקטיבית, דף שער בספרייה הלאומית
הערות שוליים
עריכה- ^ Hessenberg, Gerhard (1905), "Beweis des Desarguesschen Satzes aus dem Pascalschen", Mathematische Annalen (Berlin / Heidelberg: Springer) 61 (2): 161–172