בהסתברות ובסטטיסטיקה , התפלגות משולשת היא התפלגות רציפה עם גבול תחתון a , גבול עליון b ושכיח c , כך שמתקיים:
a
<
b
{\displaystyle a<b}
a
≤
c
≤
b
{\displaystyle a\leq c\leq b}
התפלגות משולשת
פונקציית צפיפות ההסתברות
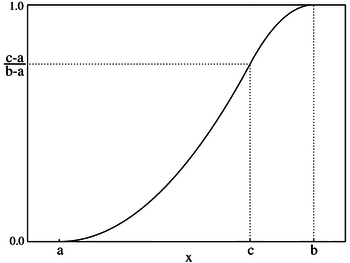
פונקציית ההסתברות המצטברת
מאפיינים
פרמטרים
a
:
a
∈
(
−
∞
,
∞
)
{\displaystyle a:~a\in (-\infty ,\infty )}
b
:
a
<
b
{\displaystyle b:~a<b\,}
c
:
a
≤
c
≤
b
{\displaystyle c:~a\leq c\leq b\,}
תומך
a
≤
x
≤
b
{\displaystyle a\leq x\leq b\!}
פונקציית צפיפות הסתברות
{
0
for
x
<
a
,
2
(
x
−
a
)
(
b
−
a
)
(
c
−
a
)
for
a
≤
x
<
c
,
2
(
b
−
x
)
(
b
−
a
)
(
b
−
c
)
for
c
≤
x
≤
b
,
0
for
b
<
x
.
{\displaystyle {\begin{cases}0&{\text{for }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{for }}a\leq x<c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{for }}c\leq x\leq b,\\[4pt]0&{\text{for }}b<x.\end{cases}}}
פונקציית ההסתברות המצטברת
{
0
for
x
≤
a
,
(
x
−
a
)
2
(
b
−
a
)
(
c
−
a
)
for
a
<
x
≤
c
,
1
−
(
b
−
x
)
2
(
b
−
a
)
(
b
−
c
)
for
c
<
x
<
b
,
1
for
b
≤
x
.
{\displaystyle {\begin{cases}0&{\text{for }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{for }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{for }}c<x<b,\\[4pt]1&{\text{for }}b\leq x.\end{cases}}}
תוחלת
a
+
b
+
c
3
{\displaystyle {\frac {a+b+c}{3}}}
חציון
{
a
+
(
b
−
a
)
(
c
−
a
)
2
for
c
≥
a
+
b
2
,
b
−
(
b
−
a
)
(
b
−
c
)
2
for
c
≤
a
+
b
2
.
{\displaystyle {\begin{cases}a+{\sqrt {\frac {(b-a)(c-a)}{2}}}&{\text{for }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\sqrt {\frac {(b-a)(b-c)}{2}}}&{\text{for }}c\leq {\frac {a+b}{2}}.\end{cases}}}
ערך שכיח
c
{\displaystyle c\,}
שונות
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
18
{\displaystyle {\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}}
אנטרופיה
1
2
+
ln
(
b
−
a
2
)
{\displaystyle {\frac {1}{2}}+\ln \left({\frac {b-a}{2}}\right)}
פונקציה יוצרת מומנטים
2
(
b
−
c
)
e
a
t
−
(
b
−
a
)
e
c
t
+
(
c
−
a
)
e
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle 2{\frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e^{bt}}{(b-a)(c-a)(b-c)t^{2}}}}
פונקציה אופיינית
−
2
(
b
−
c
)
e
i
a
t
−
(
b
−
a
)
e
i
c
t
+
(
c
−
a
)
e
i
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle -2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!-\!a)e^{ibt}}{(b-a)(c-a)(b-c)t^{2}}}}
צידוד
2
(
a
+
b
−
2
c
)
(
2
a
−
b
−
c
)
(
a
−
2
b
+
c
)
5
(
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
)
3
2
{\displaystyle {\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\!+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!-\!bc)^{\frac {3}{2}}}}}
גבנוניות
−
3
5
{\displaystyle -{\frac {3}{5}}}
ההתפלגות המשולשת מייצגת התפלגות בסיסית המבוססת רק על חסם עליון , חסם תחתון ושכיח . מהסיבות הללו, יש המכנים אותה "התפלגות של חוסר נתונים". לרוב משתמשים בהתפלגות משולשת כאשר אין מספיק נתונים וההתפלגות אינה אחידה . אולם בעיקר משתמשים בהתפלגות משולשת כאשר היחס בין המשתנים ידוע. בהתפלגות משולשת ניתן גם בקלות לחשב את ההסתברות של קבוצה בתחום, על ידי חישוב השטח שמתחת לעקומה הבנוי ממשולש . בשל מאפיינים אלו, משתמשים לרב בהתפלגות משולשת בסימולציות ובתהליכי קבלת החלטות . משתמשים גם בהתפלגות משולשת בשילוב התפלגות בטא בניהול פרויקטים .
קיימים מקרים מיוחדים בהם הנקודות הן ידועות ויש שימוש בערך מסוים של c .
ההתפלגות נהיית יותר פשוטה כאשר a =c או b =c . לדוגמה אם a =0 ו-b =c =1 אז בקטע שבו
0
≤
x
≤
1
{\displaystyle 0\leq x\leq 1}
פונקציית הצפיפות ופונקציית ההצטברות מוגדרות להיות:
f
(
x
)
=
2
x
F
(
x
)
=
x
2
{\displaystyle {\begin{aligned}f(x)&=2x\\[8pt]F(x)&=x^{2}\end{aligned}}}
E
(
X
)
=
2
3
V
a
r
(
X
)
=
1
18
{\displaystyle {\begin{aligned}E(X)&={\frac {2}{3}}\\[8pt]\mathrm {Var} (X)&={\frac {1}{18}}\end{aligned}}}
בהינתן שני משתנים מקריים בלתי תלויים, X 1 , X 2 שלשניהם התפלגות אחידה רציפה על הקטע
[
0
,
1
]
{\displaystyle [0,1]}
X = (X 1 + X 2 )/2 מתאימה למקרה שבו
a
=
0
{\displaystyle a=0}
b
=
1
{\displaystyle b=1}
c
=
0.5
{\displaystyle c=0.5}
f
(
x
)
=
{
4
x
for
0
≤
x
<
1
2
4
−
4
x
for
1
2
≤
x
≤
1
0
otherwise
{\displaystyle f(x)={\begin{cases}4x&{\text{for }}0\leq x<{\frac {1}{2}}\\4-4x&{\text{for }}{\frac {1}{2}}\leq x\leq 1\\0&{\text{otherwise}}\end{cases}}}
F
(
x
)
=
{
0
for
x
<
0
2
x
2
for
0
≤
x
<
1
2
1
−
2
(
1
−
x
)
2
for
1
2
≤
x
<
1
1
for
1
≤
x
≤
1
{\displaystyle F(x)={\begin{cases}0&{\text{for }}x<0\\2x^{2}&{\text{for }}0\leq x<{\frac {1}{2}}\\1-2(1-x)^{2}&{\text{for }}{\frac {1}{2}}\leq x<1\\1&{\text{for }}1\leq x\leq 1\\\end{cases}}}
E
(
X
)
=
1
2
Var
(
X
)
=
1
24
{\displaystyle {\begin{aligned}E(X)&={\frac {1}{2}}\\[6pt]\operatorname {Var} (X)&={\frac {1}{24}}\end{aligned}}}
עריכה
בהינתן שני משתנים מקריים בלתי תלויים, X 1 , X 2 שלשניהם התפלגות אחידה רציפה על הקטע
[
0
,
1
]
{\displaystyle [0,1]}
X
=
|
X
1
−
X
2
|
{\displaystyle X=\left|X_{1}-X_{2}\right|}
a = 0, b = 1 ו-c = 0.
f
(
x
)
=
2
−
2
x
,
for
0
≤
x
<
1
F
(
x
)
=
2
x
−
x
2
,
for
0
≤
x
<
1
E
(
X
)
=
1
3
Var
(
X
)
=
1
18
{\displaystyle {\begin{aligned}f(x)&=2-2x,{\text{ for }}0\leq x<1\\[6pt]F(x)&=2x-x^{2},{\text{ for }}0\leq x<1\\[6pt]E(X)&={\frac {1}{3}}\\[6pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}}
עריכה
כאשר נתון משתנה מקרי U שמתפלג באופן אחיד על הקטע
(
0
,
1
)
{\displaystyle (0,1)}
דגימה מהעתקה הופכית ) המשתנה
{
X
=
a
+
U
(
b
−
a
)
(
c
−
a
)
for
0
<
U
<
F
(
c
)
X
=
b
−
(
1
−
U
)
(
b
−
a
)
(
b
−
c
)
for
F
(
c
)
≤
U
<
1
{\displaystyle {\begin{matrix}{\begin{cases}X=a+{\sqrt {U(b-a)(c-a)}}&{\text{ for }}0<U<F(c)\\&\\X=b-{\sqrt {(1-U)(b-a)(b-c)}}&{\text{ for }}F(c)\leq U<1\end{cases}}\end{matrix}}}
כאשר F היא פונקציית ההתפלגות של התפלגות משולשת עם פרמטרים a, b ו-c, ומכאן שמתקיים F(c) = (c-a)/(b-a).







![{\displaystyle {\begin{cases}0&{\text{for }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{for }}a\leq x<c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{for }}c\leq x\leq b,\\[4pt]0&{\text{for }}b<x.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32b565e115f0a9727f23b3ceb84aefa9aeb9c1d9)
![{\displaystyle {\begin{cases}0&{\text{for }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{for }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{for }}c<x<b,\\[4pt]1&{\text{for }}b\leq x.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11b472d4e58e4df0814805aab0a2e752d6bdebf3)

![{\displaystyle {\begin{cases}a+{\sqrt {\frac {(b-a)(c-a)}{2}}}&{\text{for }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\sqrt {\frac {(b-a)(b-c)}{2}}}&{\text{for }}c\leq {\frac {a+b}{2}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45fe21e5d8eb394b9e5dca33a2c790c001328393)






