במתמטיקה , הפונקציות ההיפרבוליות ההפוכות הן הפונקציות ההופכיות לפונקציות ההיפרבוליות , כלומר לכל h פונקציה היפרבולית
h
(
x
)
⟹
h
−
1
(
h
(
x
)
)
=
x
{\displaystyle h(x)\Longrightarrow h^{-1}(h(x))=x}
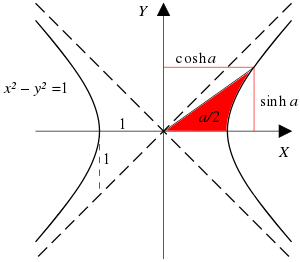
קרן דרך היפרבולת היחידה
x
2
−
y
2
=
1
{\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}
(
cosh
a
,
sinh
a
)
{\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}
הפונקציות ההיפרבוליות ההפוכות פונקציות היפרבוליות מופיעות בחישובי זוויות ומרחקים בגאומטריה היפרבולית , משוואות דיפרנציאליות , משוואות מעוקבות , ומשוואת לפלס בקואורדינטות קרטזיות . המשוואות של לפלס חשובות בתחומים רבים בפיזיקה , כולל תיאוריה אלקטרומגנטית , העברת חום , דינמיקת נוזלים, ותורת היחסות הפרטית.
סטנדרט ISO 80000-2 קובע שהשמות של הפונקציות ההיפרבוליות ההפוכות יורכבו מהתחילית ar ואחריה השמות של הפונקציות ההיפרבוליות המתאימות. לדוגמה, הפונקציה ההפוכה ל-sinh תיקרא arsinh .
ניתן למצוא גם שימוש שגוי בקידומת arc בתור אנלוגיה לשמות של הפונקציות הטריגונומטרית ההפוכות . קידומת זו לא מתאימה לפונקציות ההיפרבוליות מכיוון שהיא קיצור למילה הלטינית arcus (קשת), בעוד שהקידומת ar היא קיצור של המילה האנגלית area (שטח)[1] [2] [3]
אחרים מעדיפים להשתמש בתחילית arg, שהיא קיצור למילה הלטינית argumentum [4] a (לדוגמה asinh, acosh וכו').
הכתיב
sinh
−
1
(
x
)
{\displaystyle \sinh ^{-1}{\left(x\right)}}
[5]
פונקציות היפרבוליות הם פונקציות ממשיות על
e
x
{\displaystyle e^{x}}
נוסחה הריבועית ואז באמצעות הלוגריתם הטבעי לקבל את x.
למספרים מורכבים , הפונקציות ההיפרבוליות ההפוכות, השורש הריבועי והלוגריתם הם פונקציות רב ערכיות , ולכן עבור ערכים שונים יכול להיות שהפונקציות יחזירו את אותו ערך.
לכל הפונקציות ההיפרבוליות ההפוכות (חוץ מהקוטנגנס, הקוסכנת ההיפרבולים ההפוכים), תחום של פונקציה#תחום ההגדרה של הפונקציה הממשית קשיר .
עריכה
סינוס היפרבולי הפוך :[6] [7]
arsinh
x
=
ln
(
x
+
x
2
+
1
)
{\displaystyle \operatorname {arsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\right)}
תחום ההגדרה הוא כל הישר הממשי .
עריכה
קוסינוס היפרבולי הפוך :[6] [7]
arcosh
x
=
ln
(
x
+
x
2
−
1
)
{\displaystyle \operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)}
תחום ההגדרה:
.
x
∈
[
1
,
+
∞
)
{\displaystyle .x\in [1,+\infty )}
עריכה
טנגנס היפרבולי הפוך :[7]
artanh
x
=
1
2
ln
(
1
+
x
1
−
x
)
{\displaystyle \operatorname {artanh} x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)}
תחום ההגדרה הוא הקטע: (−1, 1) .
עריכה
קוטנגנס היפרבולי הפוך:
arcoth
x
=
1
2
ln
(
x
+
1
x
−
1
)
{\displaystyle \operatorname {arcoth} x={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)}
תחום ההגדרה הוא:
x
∈
(
−
∞
,
−
1
)
∪
(
1
,
∞
)
{\displaystyle x\in (-\infty ,-1)\cup (1,\infty )}
עריכה
הסכנת ההיפרבולי הפוך:
arsech
x
=
ln
(
1
x
+
1
x
2
−
1
)
=
ln
(
1
+
1
−
x
2
x
)
{\displaystyle \operatorname {arsech} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)}
תחום הגדרה:
x
∈
(
0
,
1
]
{\displaystyle x\in (0,1]}
עריכה
כוסכנת היפרבולי הפוך:
arcsch
x
=
ln
(
1
x
+
1
x
2
+
1
)
=
ln
(
1
+
1
+
x
2
x
)
{\displaystyle \operatorname {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)=\ln \left({\frac {1+{\sqrt {1+x^{2}}}}{x}}\right)}
תחום ההגדרה
x
∈
R
,
x
≠
0
{\displaystyle x\in R,x\neq 0}
arsinh
u
±
arsinh
v
=
arsinh
(
u
1
+
v
2
±
v
1
+
u
2
)
{\displaystyle \operatorname {arsinh} u\pm \operatorname {arsinh} v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right)}
arcosh
u
±
arcosh
v
=
arcosh
(
u
v
±
(
u
2
−
1
)
(
v
2
−
1
)
)
{\displaystyle \operatorname {arcosh} u\pm \operatorname {arcosh} v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right)}
artanh
u
±
artanh
v
=
artanh
(
u
±
v
1
±
u
v
)
{\displaystyle \operatorname {artanh} u\pm \operatorname {artanh} v=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)}
arcoth
u
±
arcoth
v
=
arcoth
(
1
±
u
v
u
±
v
)
{\displaystyle \operatorname {arcoth} u\pm \operatorname {arcoth} v=\operatorname {arcoth} \left({\frac {1\pm uv}{u\pm v}}\right)}
arsinh
u
+
arcosh
v
=
arsinh
(
u
v
+
(
1
+
u
2
)
(
v
2
−
1
)
)
=
arcosh
(
v
1
+
u
2
+
u
v
2
−
1
)
{\displaystyle {\begin{aligned}\operatorname {arsinh} u+\operatorname {arcosh} v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right)\end{aligned}}}
2
arcosh
x
=
arcosh
(
2
x
2
−
1
)
for
x
≥
1
4
arcosh
x
=
arcosh
(
8
x
4
−
8
x
2
+
1
)
for
x
≥
1
2
arsinh
x
=
arcosh
(
2
x
2
+
1
)
for
x
≥
0
4
arsinh
x
=
arcosh
(
8
x
4
+
8
x
2
+
1
)
for
x
≥
0
{\displaystyle {\begin{aligned}2\operatorname {arcosh} x&=\operatorname {arcosh} (2x^{2}-1)&\quad {\hbox{ for }}x\geq 1\\4\operatorname {arcosh} x&=\operatorname {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ for }}x\geq 1\\2\operatorname {arsinh} x&=\operatorname {arcosh} (2x^{2}+1)&\quad {\hbox{ for }}x\geq 0\\4\operatorname {arsinh} x&=\operatorname {arcosh} (8x^{4}+8x^{2}+1)&\quad {\hbox{ for }}x\geq 0\end{aligned}}}
ln
(
x
)
=
arcosh
(
x
2
+
1
2
x
)
=
arsinh
(
x
2
−
1
2
x
)
=
artanh
(
x
2
−
1
x
2
+
1
)
{\displaystyle \ln(x)=\operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)}
עריכה
sinh
(
arcosh
x
)
=
x
2
−
1
for
|
x
|
>
1
sinh
(
artanh
x
)
=
x
1
−
x
2
for
−
1
<
x
<
1
cosh
(
arsinh
x
)
=
1
+
x
2
cosh
(
artanh
x
)
=
1
1
−
x
2
for
−
1
<
x
<
1
tanh
(
arsinh
x
)
=
x
1
+
x
2
tanh
(
arcosh
x
)
=
x
2
−
1
x
for
|
x
|
>
1
{\displaystyle {\begin{aligned}&\sinh(\operatorname {arcosh} x)={\sqrt {x^{2}-1}}\quad {\text{for}}\quad |x|>1\\&\sinh(\operatorname {artanh} x)={\frac {x}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\cosh(\operatorname {arsinh} x)={\sqrt {1+x^{2}}}\\&\cosh(\operatorname {artanh} x)={\frac {1}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\tanh(\operatorname {arsinh} x)={\frac {x}{\sqrt {1+x^{2}}}}\\&\tanh(\operatorname {arcosh} x)={\frac {\sqrt {x^{2}-1}}{x}}\quad {\text{for}}\quad |x|>1\end{aligned}}}
עריכה
ln
x
=
artanh
(
x
2
−
1
x
2
+
1
)
=
arsinh
(
x
2
−
1
2
x
)
=
±
arcosh
(
x
2
+
1
2
x
)
{\displaystyle \ln x=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\pm \operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)}
artanh
x
=
arsinh
(
x
1
−
x
2
)
=
±
arcosh
(
1
1
−
x
2
)
{\displaystyle \operatorname {artanh} x=\operatorname {arsinh} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\sqrt {1-x^{2}}}}\right)}
arsinh
x
=
artanh
(
x
1
+
x
2
)
=
±
arcosh
(
1
+
x
2
)
{\displaystyle \operatorname {arsinh} x=\operatorname {artanh} \left({\frac {x}{\sqrt {1+x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\sqrt {1+x^{2}}}\right)}
arcosh
x
=
|
arsinh
(
x
2
−
1
)
|
=
|
artanh
(
x
2
−
1
x
)
|
{\displaystyle \operatorname {arcosh} x=\left|\operatorname {arsinh} \left({\sqrt {x^{2}-1}}\right)\right|=\left|\operatorname {artanh} \left({\frac {\sqrt {x^{2}-1}}{x}}\right)\right|}
d
d
x
arsinh
x
=
1
x
2
+
1
,
for all real
x
d
d
x
arcosh
x
=
1
x
2
−
1
,
for all real
x
>
1
d
d
x
artanh
x
=
1
1
−
x
2
,
for all real
|
x
|
<
1
d
d
x
arcoth
x
=
1
1
−
x
2
,
for all real
|
x
|
>
1
d
d
x
arsech
x
=
−
1
x
1
−
x
2
,
for all real
x
∈
(
0
,
1
)
d
d
x
arcsch
x
=
−
1
|
x
|
1
+
x
2
,
for all real
x
, except
0
{\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&{}={\frac {1}{\sqrt {x^{2}+1}}},{\text{ for all real }}x\\{\frac {d}{dx}}\operatorname {arcosh} x&{}={\frac {1}{\sqrt {x^{2}-1}}},{\text{ for all real }}x>1\\{\frac {d}{dx}}\operatorname {artanh} x&{}={\frac {1}{1-x^{2}}},{\text{ for all real }}|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&{}={\frac {1}{1-x^{2}}},{\text{ for all real }}|x|>1\\{\frac {d}{dx}}\operatorname {arsech} x&{}={\frac {-1}{x{\sqrt {1-x^{2}}}}},{\text{ for all real }}x\in (0,1)\\{\frac {d}{dx}}\operatorname {arcsch} x&{}={\frac {-1}{|x|{\sqrt {1+x^{2}}}}},{\text{ for all real }}x{\text{, except }}0\\\end{aligned}}}
עריכה
arsinh
x
=
x
−
(
1
2
)
x
3
3
+
(
1
⋅
3
2
⋅
4
)
x
5
5
−
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
7
7
±
⋯
=
∑
n
=
0
∞
(
(
−
1
)
n
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
2
n
+
1
2
n
+
1
,
|
x
|
<
1
{\displaystyle {\begin{aligned}\operatorname {arsinh} x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}}
arcosh
x
=
ln
(
2
x
)
−
(
(
1
2
)
x
−
2
2
+
(
1
⋅
3
2
⋅
4
)
x
−
4
4
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
−
6
6
+
⋯
)
=
ln
(
2
x
)
−
∑
n
=
1
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
−
2
n
2
n
,
|
x
|
>
1
{\displaystyle {\begin{aligned}\operatorname {arcosh} x&=\ln(2x)-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln(2x)-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{2n}},\qquad \left|x\right|>1\end{aligned}}}
artanh
x
=
x
+
x
3
3
+
x
5
5
+
x
7
7
+
⋯
=
∑
n
=
0
∞
x
2
n
+
1
2
n
+
1
,
|
x
|
<
1
{\displaystyle {\begin{aligned}\operatorname {artanh} x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}}
arcsch
x
=
arsinh
1
x
=
x
−
1
−
(
1
2
)
x
−
3
3
+
(
1
⋅
3
2
⋅
4
)
x
−
5
5
−
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
−
7
7
±
⋯
=
∑
n
=
0
∞
(
(
−
1
)
n
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
−
(
2
n
+
1
)
2
n
+
1
,
|
x
|
>
1
{\displaystyle {\begin{aligned}\operatorname {arcsch} x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}}
arsech
x
=
arcosh
1
x
=
ln
2
x
−
(
(
1
2
)
x
2
2
+
(
1
⋅
3
2
⋅
4
)
x
4
4
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
6
6
+
⋯
)
=
ln
2
x
−
∑
n
=
1
∞
(
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
2
n
2
n
,
0
<
x
≤
1
{\displaystyle {\begin{aligned}\operatorname {arsech} x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\end{aligned}}}
arcoth
x
=
artanh
1
x
=
x
−
1
+
x
−
3
3
+
x
−
5
5
+
x
−
7
7
+
⋯
=
∑
n
=
0
∞
x
−
(
2
n
+
1
)
2
n
+
1
,
|
x
|
>
1
{\displaystyle {\begin{aligned}\operatorname {arcoth} x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3}}{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}}
arsinh
x
=
ln
(
2
x
)
+
∑
n
=
1
∞
(
−
1
)
n
−
1
(
2
n
−
1
)
!
!
2
n
(
2
n
)
!
!
1
x
2
n
{\displaystyle \operatorname {arsinh} x=\ln(2x)+\sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\frac {\left({2n-1}\right)!!}{2n\left({2n}\right)!!}}}{\frac {1}{x^{2n}}}}
כפונקציות של משתנה מורכב , פונקציות היפרבוליות הפוכות הן פונקציות רב ערכיות שהן אנליטיות , למעט במספר סופי של נקודות.
מפני שהפונקציות הן רב ערכיות במישור המורכב אז כמו בפונקציות טריגונומטריות הפוכות מעדיפים להגדיר אותם רק מעל תחום מסוים בו הן חד ערכיות.
עריכה
ההגדרה של הסינוס ההיפרבולי ההפוך במישור המורכב ניתן על ידי
arsinh
z
=
Log
(
z
+
z
2
+
1
)
.
{\displaystyle \operatorname {arsinh} z=\operatorname {Log} (z+{\sqrt {z^{2}+1}}\,)\,.}
התוצאה השורש הריבועי הוא מספר ממשי שאינו חיובי, אם ורק אם
z
∈
(
−
∞
i
,
−
i
)
∪
(
i
,
∞
)
{\displaystyle z\in (-\infty i,-i)\cup (i,\infty )}
עריכה
arcosh
z
=
Log
(
z
+
z
+
1
z
−
1
)
.
{\displaystyle \operatorname {arcosh} z=\operatorname {Log} (z+{\sqrt {z+1}}{\sqrt {z-1}}\,)\,.}
עריכה
artanh
z
=
1
2
Log
(
1
+
z
1
−
z
)
arcoth
z
=
1
2
Log
(
z
+
1
z
−
1
)
{\displaystyle {\begin{aligned}\operatorname {artanh} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {1+z}{1-z}}\right)\\\operatorname {arcoth} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {z+1}{z-1}}\right)\end{aligned}}}
^ As stated by Jan Gullberg , Mathematics: From the Birth of Numbers (New York: W. W. Norton & Company , 1997), ISBN 0-393-04002-X Another form of notation, arcsinh x , arccosh x , etc., is a practice to be condemned as these functions have nothing whatever to do with arc, but with area, as is demonstrated by their full Latin names,
arsinh area sinus hyperbolicus
arcosh area cosinus hyperbolicus, etc.
^ As stated by Eberhard Zeidler , Wolfgang Hackbusch and Hans Rudolf Schwarz, translated by Bruce Hunt, Oxford Users' Guide to Mathematics Oxford University Press , 2004), ISBN 0-19-850763-1 x ). ..." This aforesaid reference uses the notations arsinh, arcosh, artanh, and arcoth for the respective inverse hyperbolic functions.
^ As stated by Ilja N. Bronshtein , Konstantin A. Semendyayev , Gerhard Musiol and Heiner Mühlig, Handbook of Mathematics Springer-Verlag , 5th ed., 2007), ISBN 3-540-72121-5 doi :10.1007/978-3-540-72122-2 , Section 2.10: "Area Functions", p. 91:
The area functions are the inverse functions of the hyperbolic functions, i.e., the inverse hyperbolic functions . The functions sinh x , tanh x , and coth x are strictly monotone, so they have unique inverses without any restriction; the function cosh x has two monotonic intervals so we can consider two inverse functions. The name area refers to the fact that the geometric definition of the functions is the area of certain hyperbolic sectors ...
^ Harold Maile Bacon, Differential and Integral Calculus: By Harold Maile Bacon ... (באנגלית)
^ Eric W. Weisstein, Inverse Hyperbolic Functions , mathworld.wolfram.com (באנגלית)
^ 1 2 Weisstein, Eric W. "Inverse Hyperbolic Functions" . mathworld.wolfram.com (באנגלית). נבדק ב-2020-08-30 . ^ 1 2 3 "Inverse hyperbolic functions - Encyclopedia of Mathematics" . encyclopediaofmath.org . נבדק ב-2020-08-30 .