טרפז

טְרָפֶּז הוא מרובע שיש לו זוג צלעות נגדיות מקבילות.

טרפז

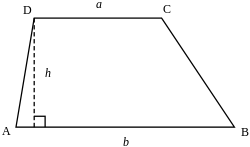
בטרפז שאינו מקבילית, שתי הצלעות המקבילות נקראות "בסיסי הטרפז" (לפעמים קרויה "בסיס" רק הצלע הארוכה יותר), ושתי האחרות "שוקי הטרפז". בטרפז כזה ניתן להמשיך את שוקי הטרפז עד שהן ייפגשו בנקודה, ובצורה זו נוצר משולש המכיל את הטרפז. הזוויות הסמוכות לכל אחד מהבסיסים נקראות זוויות הבסיס.

קטע אמצעים בטרפז, הוא קטע אשר מחבר בין אמצעי שוקי הטרפז. קטע האמצעים בטרפז מקביל לבסיסי הטרפז ואורכו הוא ממוצע האורכים שלהם.

מרובע הוא טרפז אם ורק אם יש לו שתי זוויות סמוכות שסכומן 180 מעלות.

אטימולוגיה

מקור המונח "טרפז" במונח היווני τραπέζιον, טרפזיון, שמשמעותו "שולחן קטן". זוהי צורת ההקטנה של τράπεζα, טרפזה, שמשמעותו "שולחן". גם המילה "טרפזה" מורכבת משתי מילים: τετράς, טטרס (ארבע) ו-πέζα, פזה (רגל), כלומר "טרפזה" משמעו "בעל ארבע רגליים".

הגדרה מצמצמת לטרפז

מקורות רבים העוסקים בגאומטריה (ובהם האנציקלופדיה העברית והאתר של משרד החינוך בישראל), מגדירים טרפז כ"מרובע שבו יש זוג יחיד של צלעות המקבילות זו לזו" (או, "מרובע אשר לו זוג אחד בלבד של צלעות מקבילות"). הגדרה זו מוציאה את המקבילית ממשפחת הטרפזים, ויש לה מספר חסרונות בולטים:

משפחות מרובעים: מן הכלל אל הפרט

• בעוד שכל ריבוע הוא סוג מיוחד של מלבן וכל מעוין הוא סוג מיוחד של דלתון, הרי על-פי ההגדרה המצמצמת, המקבילית איננה טרפז. בין משפחות המרובעים שוררים יחסי הכלה, וההגדרה המצמצמת הופכת את הטרפזים לחריג.
• שוויון הנכון לכל הטרפזים (במובן הצר) נכון תמיד גם עבור מקביליות. ההגדרה שהובאה בתחילת הערך מאפשרת לנסח את שתי התוצאות במשפט אחד, בעוד שבהגדרה המצמצמת יש צורך לחזור על הטענה (וההוכחה) פעמיים.
• כל סוגי המרובעים מוגדרים על-פי שוויון (צלעות שוות, זוויות שוות, זווית ישרה), ורק הגדרה מצמצמת של הטרפז תדרוש אי-שוויון.
• הסעת קודקוד אחד של הטרפז לאורך אחת הצלעות המקבילות תשמור על תכונות הטרפז עד ששניים מקודקודיו מתלכדים. הגדרה מצמצמת תוסיף לתהליך כזה נקודה מיוחדת שבה הטרפז חדל לרגע מלהיות טרפז - תופעה שאין לה אח ורע במשפחות המרובעים האחרות (וגם לא בהגדרות גאומטריות כלליות יותר).

עם כל זאת, יודגש שאין משמעות לשאלה איזו הגדרה "נכונה" יותר. הגדרות (המנוסחות כראוי) אינן יכולות להיות נכונות או שגויות - הגדרה נבחנת בכך שהיא מפשטת את הדיון במונחים שאליהם היא מתייחסת.

שטח

את שטח הטרפז ניתן לחשב כמכפלת המרחק בין שתי הצלעות המקבילות (זהו גובה הטרפז) והממוצע החשבוני של אורך הצלעות הללו. כך ניתן להגיע לנוסחה הידועה של שטח משולש, כאשר אנו מחשיבים את המשולש כטרפז בו אחת הצלעות המקבילות מכווצת לנקודה בודדת (כלומר בעלת אורך 0). נוסחאות לחישוב שטח טרפז כלשהו (כאשר a,b מציינים בסיסים; ו-c,d מציינים צלעות):

$S={\frac {(a+b)h}{2}}$

או

$S={\frac {a+c}{4(a-c)}}{\sqrt {(a+b-c+d)(a-b-c+d)(a+b-c-d)(-a+b+c+d)}}$

כאשר a,b,c,d צלעות טרפז.

האלכסונים יוצרים ארבעה משולשים: מכפלת שטח שני המשולשים הנוצרים עם הבסיסים שווה למכפלת שטח שני המשולשים הנוצרים עם השוקיים.

טרפזים מיוחדים

טרפז נקרא שווה-שוקיים אם זוויות הבסיס שלו שוות. בטרפז שווה-שוקיים שתי השוקיים שוות באורכן ושני האלכסונים שווים. טרפז שבו שתי השוקיים שוות באורכן הוא טרפז שווה-שוקיים או מקבילית. כל טרפז החסום במעגל הוא שווה-שוקיים משום שסכום הזוויות הנגדיות בכל מרובע החסום במעגל שווה ל-180 מעלות.

טרפז ישר-זווית

טרפז נקרא ישר-זווית אם יש לו שתי זוויות השוות כל אחת ל90 מעלות. במקרה זה, גובה הטרפז הוא השוק עליה נשענות שתי הזוויות הישרות.

קישורים חיצוניים

• הגדרות שונות ל"אותו מושג" – מנוף או מכשול? המקרה של הטרפז, קרני שיר ואורית זסלבסקי, על"ה 54 | אוגוסט 2016
• טרפז, באתר MathWorld (באנגלית)